Bevezetés a Statikába: A Mérnöki Mechanika Alapköve
A statika a mérnöki mechanika egyik alapvető ága, amely a nyugalomban lévő vagy egyenletes sebességgel mozgó testekre ható erők és nyomatékok egyensúlyával foglalkozik. Ez a tudományág elengedhetetlenül fontos az építőmérnökök, gépészmérnökök és más mérnöki területeken dolgozó szakemberek számára, hiszen a tartószerkezetek, gépek és egyéb mérnöki alkotások tervezése és elemzése során a statikai elvek alkalmazása nélkülözhetetlen a biztonság, a stabilitás és a funkcionalitás biztosításához. A statikai feladatok megoldása nem csupán matematikai és fizikai ismereteket igényel, hanem a mérnöki szemléletmód és a problémamegoldó képesség magas szintű birtoklását is.
Ebben az átfogó útmutatóban részletesen bemutatjuk a statika alapelveit, a különböző erőrendszereket, az egyensúly feltételeit, a támaszerők számításának módszereit, a nyomaték fogalmát és annak alkalmazását, valamint a gyakran előforduló statikai szerkezetek, mint például a rácsos tartók és a gerendák elemzését. Emellett érintjük az összetett szerkezetek megoldásának speciális módszereit, a virtuális munka elvét, a potenciális energia elvét, a statikai határozatlanság kérdéskörét és a számítógépes módszerek szerepét a modern statikai analízisben. Célunk, hogy egy olyan részletes és érthető forrást nyújtsunk, amely mind a mérnökhallgatók, mind a gyakorló mérnökök számára értékes segítséget jelent a statikai feladatok megoldása során.
A Statika Alapelvei és Meghatározó Fogalmai

A statika megértéséhez és a statikai feladatok sikeres megoldásához elengedhetetlen a néhány alapvető elv és fogalom tisztázása. Ezek az alapelvek képezik a statikai analízis és a tartószerkezetek tervezésének fundamentumát. A legfontosabb alapelvek közé tartozik a Newton első törvénye, amely kimondja, hogy egy test nyugalomban marad vagy egyenes vonalú egyenletes mozgást végez mindaddig, amíg külső erő nem hat rá. A statika szempontjából ez azt jelenti, hogy egy egyensúlyban lévő testre ható erők eredője és az erre ható nyomatékok eredője egyaránt nulla.
Egy másik kulcsfontosságú fogalom az erő, amely egy fizikai mennyiség, ami egy test mozgásállapotának megváltoztatására vagy alakjának deformálására törekszik. Az erő vektormennyiség, azaz rendelkezik nagysággal, iránnyal és hatásvonallal. A statikai feladatok során gyakran találkozunk különböző típusú erőkkel, mint például a pontszerű erők, az elosztott terhelések (lineárisan változó, egyenletes stb.), a súlyerő, a támaszerők és a reakcióerők. A helyes erődiagramok (szabadtest diagramok) elkészítése az első és legfontosabb lépés a statikai feladatok megoldásában.
A nyomaték egy olyan fizikai mennyiség, amely egy erő forgató hatását írja le egy adott tengely vagy pont körül. A nyomaték nagysága az erő nagyságának és az erő hatásvonalának a forgási tengelytől vagy ponttól mért merőleges távolságának (erőkar) a szorzata. A statikai egyensúly szempontjából nem csak az erők eredőjének, hanem a nyomatékok eredőjének is nullának kell lennie. A nyomatékok helyes értelmezése és számítása kritikus fontosságú a tartószerkezetek stabilitásának és a csavaró igénybevételeknek a vizsgálatában.
A merev test fogalma szintén alapvető a statikában. Egy merev test olyan idealizált test, amelynek alakja és méretei a rá ható erők hatására nem változnak meg. Bár a valóságban nincsenek tökéletesen merev testek, sok mérnöki alkalmazásban a deformációk olyan kicsik, hogy a testeket jó közelítéssel merevnek tekinthetjük. Ez az egyszerűsítés lehetővé teszi a statikai feladatok kezelhető matematikai modellekkel történő leírását és megoldását.
Végül, a szabadtest diagram (szabadtest ábra) egy olyan rajz, amely egy vizsgált testet vagy szerkezetet izoláltan ábrázol, feltüntetve az összes rá ható külső erőt és nyomatékot. A szabadtest diagram elkészítése elengedhetetlen a statikai egyensúly egyenleteinek felírásához és a ismeretlen erők (pl. támaszerők, belső erők) meghatározásához. A szabadtest diagram helyes megrajzolása a statikai feladatok megoldásának egyik legkritikusabb lépése, amely megköveteli a rendszer határainak pontos azonosítását és az összes külső hatás figyelembevételét.
Erőrendszerek és azok Meghatározó Jellemzői a Statikában

A statikai feladatok során különböző típusú erőrendszerekkel találkozhatunk, amelyek mindegyike sajátos jellemzőkkel rendelkezik és speciális megközelítést igényel a megoldás során. Az erőrendszer egy testre vagy szerkezetre ható erők és nyomatékok összessége. Az erőrendszereket aszerint csoportosíthatjuk, hogy az erők milyen módon helyezkednek el a térben és hogyan hatnak a testre.
Az egyik legegyszerűbb erőrendszer a konkurrens erőrendszer, amelyben az összes erő hatásvonala egyetlen közös pontban metszik egymást. Ilyen erőrendszerrel találkozhatunk például egy csomópontban összetalálkozó rudak esetén egy rácsos tartóban. A konkurrens erőrendszerek egyensúlyának feltétele, hogy az erők vektoros összege nulla legyen. Két dimenzióban ez két skaláris egyenletet jelent (\\sum F\_x \= 0 és \\sum F\_y \= 0), míg három dimenzióban három egyenletet (\\sum F\_x \= 0, \\sum F\_y \= 0 és \\sum F\_z \= 0).
Egy másik fontos erőrendszer a párhuzamos erőrendszer, amelyben az összes erő hatásvonala párhuzamos egymással. Ilyen erőrendszerrel találkozhatunk például egy gerendára ható egyenletes eloszlású terhelés esetén (ha a terhelés iránya merőleges a gerendára). A párhuzamos erőrendszerek egyensúlyának feltétele, hogy az erők eredője nulla legyen, és a nyomatékok eredője egy tetszőleges pontra nézve szintén nulla legyen.

Az általános térbeli erőrendszer a legkomplexebb eset, amelyben az erők hatásvonalai tetszőlegesen helyezkedhetnek el a térben és nem feltétlenül metszik egymást vagy párhuzamosak. Egy általános térbeli erőrendszer egyensúlyának feltétele, hogy az erők eredőjének mindhárom komponense nulla legyen (\\sum F\_x \= 0, \\sum F\_y \= 0, \\sum F\_z \= 0), és a nyomatékok eredőjének is mindhárom komponense nulla legyen egy tetszőleges pontra nézve (\\sum M\_x \= 0, \\sum M\_y \= 0, \\sum M\_z \= 0).
A statikai feladatok megoldása során gyakran alkalmazzuk az erők eredőjének és az eredő nyomatékának a fogalmát. Az erők eredője az az egyetlen erő, amely ugyanazt a transzlációs hatást fejti ki a testre, mint az eredeti erőrendszer. A nyomatékok eredője pedig az az egyetlen nyomaték, amely ugyanazt a rotációs hatást fejti ki a testre, mint az eredeti erőrendszer. Az egyensúly feltétele az, hogy mind az erők eredője, mind a nyomatékok eredője nulla legyen.
Az erőrendszerek elemzése során fontos a vektoralgebra alapjainak ismerete, beleértve az erők felbontását komponensekre, az erők összeadását, a skalárszorzatot és a vektori szorzatot (amely a nyomaték számításához elengedhetetlen). A helyes koordináta-rendszer megválasztása szintén nagyban megkönnyítheti a statikai feladatok megoldását, különösen a térbeli esetekben.
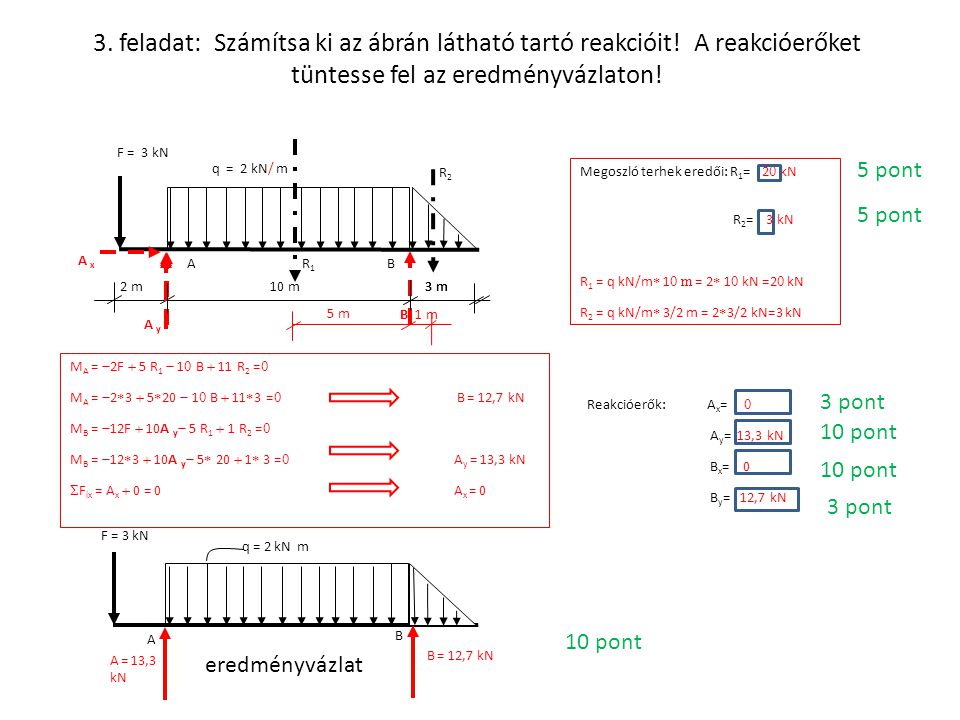
Az Egyensúly Feltételei a Statikában: A Stabilitás Záloga
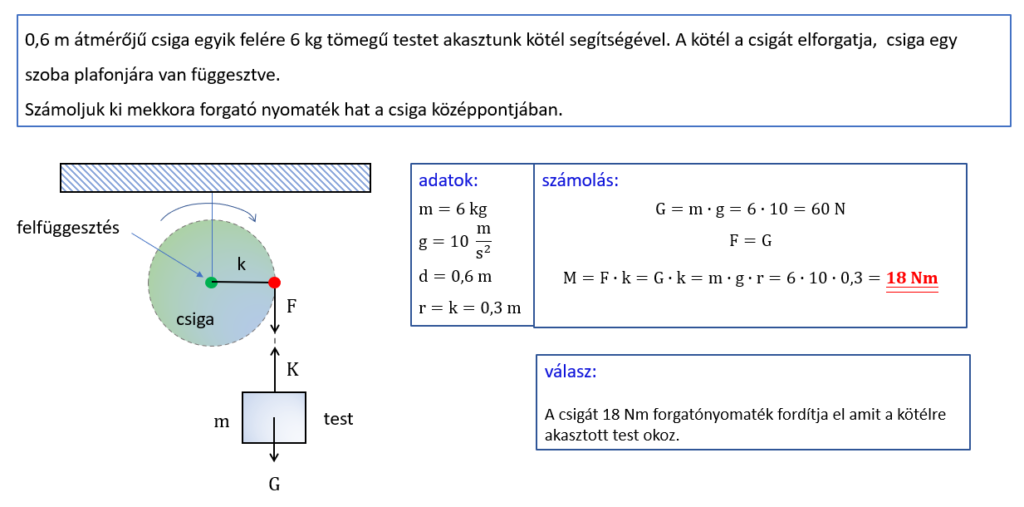
A statika központi fogalma az egyensúly. Egy test vagy szerkezet akkor van statikai egyensúlyban, ha nyugalomban van, vagy egyenes vonalú egyenletes mozgást végez, és ez az állapota külső hatásokra nem változik meg. A statikai egyensúly biztosítása a tartószerkezetek és gépek tervezésének egyik legfontosabb célja, hiszen ez garantálja a biztonságos és megbízható működést.
Az egyensúly feltételei matematikai formában is megfogalmazhatók. Egy kétdimenziós (sík) erőrendszer esetén a statikai egyensúly három független egyenlettel írható le:
\\sum F\_x \= 0
\\sum F\_y \= 0
\\sum M\_O \= 0
Ahol \\sum F\_x a vízszintes irányú erők összegét, \\sum F\_y a függőleges irányú erők összegét, és \\sum M\_O az egy tetszőleges O pontra vonatkozó nyomatékok összegét jelenti. Ezeknek az összegeknek nullának kell lenniük ahhoz, hogy a test vagy szerkezet egyensúlyban legyen.

Egy háromdimenziós (térbeli) erőrendszer esetén a statikai egyensúly hat független egyenlettel írható le:
\\sum F\_x \= 0, \\quad \\sum F\_y \= 0, \\quad \\sum F\_z \= 0
\\sum M\_x \= 0, \\quad \\sum M\_y \= 0, \\quad \\sum M\_z \= 0
Ahol \\sum F\_x, \\sum F\_y, \\sum F\_z az erők összegének komponenseit a x, y, z