Keresztmetszet Atmero Atvaltas

A Keresztmetszet és az Átmérő közötti Átváltás részletes útmutatója

Üdvözöljük átfogó útmutatónkban, amely a keresztmetszet és az átmérő közötti átváltás rejtelmeibe vezeti be Önt. Legyen szó mérnöki tervezésről, építőipari munkálatokról vagy akár csak egy otthoni barkácsprojektről, a kör alakú objektumok keresztmetszetének és átmérőjének pontos ismerete elengedhetetlen. Ebben a részletes cikkben nem csupán a matematikai alapokat fogjuk tisztázni, hanem gyakorlati példákon keresztül is bemutatjuk, hogyan végezheti el a szükséges számításokat.

A Keresztmetszet fogalma és jelentősége

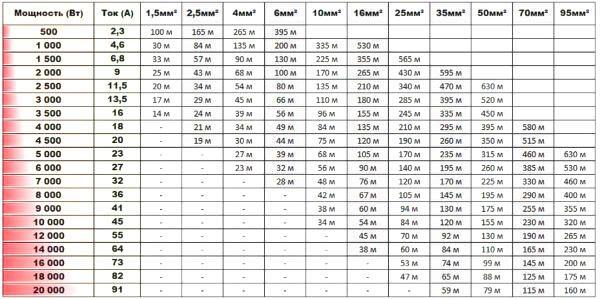
A keresztmetszet egy objektum, jelen esetben egy kör alakú test, egy adott síkkal való metszésének területe. Különösen fontos fogalom ez a mechanikában, az anyagtanban, a folyadékok és gázok áramlásának tanulmányozásában, valamint az elektromos vezetők méretezésénél. A megfelelő keresztmetszet biztosítja a szerkezetek szilárdságát, a vezetők áramhordozó képességét és a folyadékok optimális áramlását.

Miért fontos a keresztmetszet ismerete?

A keresztmetszet ismerete számos területen kritikus fontosságú:

Statika és szilárdságtan: A terhelések elviseléséhez szükséges anyagmennyiség meghatározásakor.
Hidraulika és pneumatika: A csővezetékek áramlási sebességének és nyomásveszteségének számításakor.
Elektrotechnika: A vezetékek áramterhelhetőségének és ellenállásának meghatározásakor.
Építészet: A tartószerkezetek, például oszlopok és gerendák méretezésénél.

Az Átmérő definíciója és kapcsolata a sugárral

A kör átmérője a kör középpontján áthaladó olyan egyenes szakasz, amelynek mindkét végpontja a körvonalon fekszik. Az átmérő a kör két legtávolabbi pontját köti össze, és hossza kétszerese a kör sugarának (r). Ezt a következő egyszerű képlettel fejezhetjük ki:

d = 2r

ahol:

d az átmérő
r a sugár

A sugár szerepe a számításokban

A sugár a kör középpontjától a körvonal bármely pontjáig húzott egyenes szakasz. Számos geometriai számítás alapját képezi, beleértve a keresztmetszet (terület) meghatározását is.

A Keresztmetszet kiszámítása az Átmérőből

Kör alakú objektumok esetén a keresztmetszet (terület) kiszámításához az alábbi képletet használjuk, ha az átmérő (d) ismert:

A = π * (d/2)²

vagy másképpen:

A = π * r²

ahol:

A a keresztmetszet (terület)
π (pi) egy matematikai konstans, értéke megközelítőleg 3,14159
d az átmérő
r a sugár (ami az átmérő fele: r = d/2)

Lépésről lépésre a számítás

Mérje meg a kör alakú objektum átmérőjét.
Ossza el az átmérőt kettővel, hogy megkapja a sugarat.
Négyzetre emelje a sugár értékét.
Szorozza meg a kapott értéket π-vel (körülbelül 3,14159).
Az eredmény a kör keresztmetszete (területe).

Az Átmérő kiszámítása a Keresztmetszetből

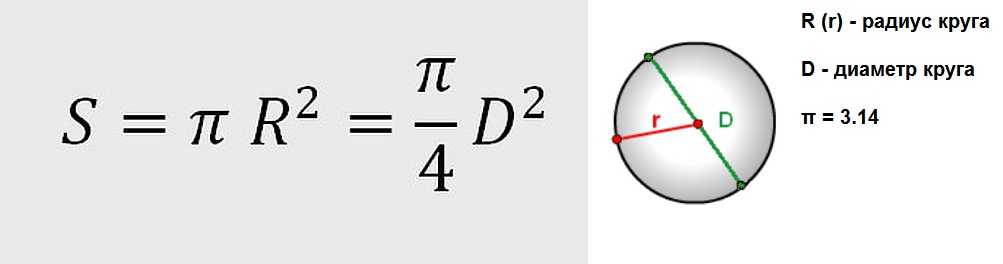
Ha a kör alakú objektum keresztmetszete (területe) ismert, az átmérő (d) a következőképpen számítható ki:

d = 2 * √(A / π)

ahol:

d az átmérő
A a keresztmetszet (terület)
π (pi) egy matematikai konstans, értéke megközelítőleg 3,14159
√ a négyzetgyököt jelöli

Lépésről lépésre a számítás

Ismerje a kör alakú objektum keresztmetszetét (területét).
Ossza el a keresztmetszet értékét π-vel (körülbelül 3,14159).
Vonjon négyzetgyököt a kapott értékből.
Szorozza meg a négyzetgyök eredményét kettővel.
Az eredmény a kör átmérője.

Gyakorlati példák az átváltásra

Példa 1: Átmérőből keresztmetszet számítása

Tegyük fel, hogy egy kábel átmérője 10 mm. Számítsuk ki a keresztmetszetét.

Átmérő (d) = 10 mm
Sugár (r) = d / 2 = 10 mm / 2 = 5 mm
Keresztmetszet (A) = π * r² = π * (5 mm)² ≈ 3,14159 * 25 mm² ≈ 78,54 mm²

Tehát a kábel keresztmetszete körülbelül 78,54 négyzetmilliméter.

Példa 2: Keresztmetszetből átmérő számítása

Egy cső keresztmetszete 50 cm². Számítsuk ki az átmérőjét.

Keresztmetszet (A) = 50 cm²
A / π = 50 cm² / 3,14159 ≈ 15,915 cm²
√(A / π) ≈ √15,915 cm² ≈ 3,989 cm
Átmérő (d) = 2 * √(A / π) ≈ 2 * 3,989 cm ≈ 7,978 cm

Tehát a cső átmérője körülbelül 7,978 centiméter.

Fontos megjegyzések és gyakori hibák

Mindig ügyeljen a mértékegységekre. Ha az átmérőt milliméterben adta meg, a keresztmetszet négyzetmilliméterben lesz.
A π értékét a számítások során a lehető legnagyobb pontossággal használja. A számológépek általában tárolják a π pontosabb értékét.
Ne keverje össze a sugarat és az átmérőt a képletekben.
Ellenőrizze a számításokat, különösen összetettebb feladatoknál.

Mértékegységek közötti átváltás

Gyakran előfordul, hogy a mértékegységeket is át kell váltani a számítások során. Például, ha az átmérőt centiméterben adták meg, de a keresztmetszetet négyzetmilliméterben szeretné megkapni, először át kell váltania a centimétert milliméterre (1 cm = 10 mm), vagy fordítva.

Összefoglalás

A keresztmetszet és az átmérő közötti átváltás alapvető fontosságú számos műszaki és gyakorlati területen. A megfelelő képletek és a pontos számítási lépések ismeretében könnyedén elvégezheti ezeket a konverziókat. Reméljük, hogy ez a részletes útmutató minden kérdésére választ adott, és most már magabiztosan alkalmazhatja a tanultakat a saját projektjeiben.

További források és segítség

Ha további kérdései merülnek fel, vagy mélyebben szeretne elmerülni a témában, javasoljuk, hogy tekintse meg a kapcsolódó műszaki kézikönyveket és online kalkulátorokat. Ne feledje, a pontos számítások elengedhetetlenek a biztonságos és hatékony munkavégzéshez.

Uncategorized

Muraszta Elado

Mi is pontosan a muraszta és miért olyan népszerű?

A muraszta egy rendkívül tartós és sokoldalú faanyag, amelyet évszázadok óta nagyra becsülnek kiváló tulajdonságai miatt. A muraszta név valójában nem egy konkrét fafajtát jelöl, hanem egy technológiai eljárással kezelt, keményfából készült terméket. Leggyakrabban tölgyből, bükkből vagy akácból készül, de más keményfa fajták is felhasználásra kerülhetnek. A lényeg a speciális hőkezelési eljárásban rejlik, amelynek köszönhetően a faanyag jelentősen javítja a tulajdonságait.

A muraszta népszerűségének több oka is van. Először is, a hőkezelés következtében a faanyag sokkal ellenállóbbá válik a nedvességgel, a gombákkal és a rovarokkal szemben. Ezáltal élettartama jelentősen megnő, ami hosszú távon költséghatékony megoldást jelent. Másodszor, a muraszta rendkívül kemény és kopásálló, így ideális választás olyan helyekre, ahol nagy a mechanikai igénybevétel, például teraszburkolatokhoz vagy padlózatokhoz. Harmadszor, a hőkezelés a faanyag esztétikai megjelenését is javítja. A muraszta általában sötétebb, gazdagabb színű és egyenletesebb textúrájú, ami elegáns és természetes megjelenést kölcsönöz a felhasználási területnek.

A muraszta készítésének részletes folyamata

A muraszta előállítása egy gondosan ellenőrzött, többlépcsős folyamat, amelynek során a kiválasztott keményfa alapanyag speciális hőkezelésen esik át. Ez a folyamat kulcsfontosságú a muraszta egyedülálló tulajdonságainak kialakításához.

1. A nyersanyag kiválasztása és előkészítése

A muraszta készítésének első lépése a megfelelő minőségű keményfa alapanyag kiválasztása. A leggyakrabban használt fafajták a tölgy, a bükk és az akác, de fontos, hogy a faanyag egészséges, csomómentes és megfelelő nedvességtartalommal rendelkezzen. A kiválasztott rönköket fűrésztelepeken feldolgozzák a kívánt méretű és formájú deszkákká vagy lécekké.

2. A szárítási folyamat

A frissen vágott faanyag nedvességtartalma általában magas, ezért a hőkezelés előtt alaposan ki kell szárítani. A szárítási folyamat során a faanyagot speciális szárítókamrákban, kontrollált hőmérsékleten és páratartalom mellett fokozatosan csökkentik a nedvességtartalmát az optimális szintre. Ez a lépés elengedhetetlen a későbbi vetemedések és repedések elkerülése érdekében.

3. A hőkezelési eljárás

A muraszta készítésének legfontosabb szakasza a hőkezelési eljárás. A megfelelően szárított faanyagot speciális hőkamrákba helyezik, ahol magas hőmérsékletnek (általában 160-240 °C között) és gőznek vagy inert gáznak teszik ki meghatározott ideig. A hőkezelés pontos paraméterei (hőmérséklet, időtartam, gőz mennyisége) a kívánt tulajdonságoktól és a felhasznált fafajtától függenek. A magas hőmérséklet hatására a faanyagban kémiai változások következnek be. A hemicellulóz tartalma csökken, ami jelentősen javítja a faanyag biológiai ellenállóképességét. Emellett a faanyag szerkezete is megváltozik, ami növeli a keménységét és a stabilitását.

4. A hűtési és kondicionálási fázis

A hőkezelés befejezése után a muraszta lassan lehűtik és kondicionálják. Ez a lépés azért fontos, hogy a faanyag stabilizálódjon és elkerüljék a hirtelen hőmérsékletváltozás okozta károkat. A kondicionálás során a faanyag visszanyeri a megfelelő nedvességtartalmát, ami biztosítja a hosszú távú stabilitást.

5. A végleges megmunkálás és minőségellenőrzés

A lehűlt és kondicionált muraszta ezt követően a végleges megmunkálási folyamatokon megy keresztül. Ide tartozhat a gyalulás, a csiszolás, a méretre vágás és a felületkezelés (például olajozás vagy viaszolás). A gyártási folyamat utolsó lépése a szigorú minőségellenőrzés, amely biztosítja, hogy a muraszta termékek megfeleljenek a legmagasabb minőségi követelményeknek.

A muraszta különböző fajtái és sokoldalú felhasználási területei

A muraszta sokoldalúsága abban rejlik, hogy különböző fafajtákból készülhet, és ennek köszönhetően széles körben alkalmazható a különböző építészeti és kerti projektekben.

Tölgy muraszta: A klasszikus elegancia és tartósság

A tölgy muraszta az egyik legnépszerűbb választás a kiváló keménysége, kopásállósága és jellegzetes, gyönyörű erezete miatt. A hőkezelés a tölgy színét mélyebbé és gazdagabbá teszi, kiemelve annak természetes szépségét. A tölgy muraszta ideális választás padlózatokhoz, lépcsőkhöz, teraszburkolatokhoz és egyéb olyan helyekre, ahol a tartósság és az esztétikai megjelenés egyaránt fontos.

Bükk muraszta: A modern és letisztult megjelenés

A bükk muraszta világosabb színével és egyenletesebb textúrájával modern és letisztult megjelenést kölcsönöz a térnek. A hőkezelés a bükköt is keményebbé és ellenállóbbá teszi, így kiválóan alkalmas belsőépítészeti alkalmazásokra, például padlózatokra, falburkolatokra és bútorokhoz.

Akác muraszta: A természetes ellenállóság és a robusztus megjelenés

Az akác muraszta természetesen is rendkívül tartós és ellenálló a nedvességgel és a rovarokkal szemben. A hőkezelés tovább fokozza ezeket a tulajdonságait, miközben a faanyag sötétebb, markánsabb megjelenést kap. Az akác muraszta különösen népszerű kültéri alkalmazásokhoz, például kerítésekhez, kerti bútorokhoz és teraszburkolatokhoz.

Egyéb keményfa muraszta fajták

A tölgy, bükk és akác mellett más keményfa fajtákból is készülhet muraszta, mint például a kőris vagy a juhar. Ezek a fajták is rendelkeznek egyedi tulajdonságokkal és megjelenéssel, így a felhasználók széles választékból választhatnak az igényeiknek leginkább megfelelőt.

A muraszta sokoldalú felhasználási területei

Teraszburkolatok: A muraszta kiválóan ellenáll az időjárás viszontagságainak, a nedvességnek és a kopásnak, így ideális választás teraszok burkolására.
Kerítések: A tartós és esztétikus muraszta kerítések hosszú éveken át megőrzik szépségüket és védelmüket.
Padlózatok: A muraszta padlók rendkívül kemények és kopásállóak, emellett meleg és természetes hangulatot teremtenek.
Homlokzatburkolatok: A muraszta homlokzatburkolatok elegáns megjelenést kölcsönöznek az épületeknek, miközben védelmet nyújtanak az időjárás ellen.
Kerti bútorok: A muraszta kerti bútorok tartósak, időjárásállóak és kényelmesek.
Lépcsők és korlátok: A muraszta lépcsők és korlátok masszívak, biztonságosak és esztétikusak.
Egyéb faipari termékek: A muraszta felhasználható még sok más faipari termék gyártására is, például falburkolatokra, lambériákra és dekorációs elemekre.

A muraszta kiemelkedő előnyös tulajdonságai

A muraszta számos olyan előnyös tulajdonsággal rendelkezik, amelyek miatt ideális választás a legkülönbözőbb projektekhez.

Kiváló tartósság és hosszú élettartam

A hőkezelési eljárásnak köszönhetően a muraszta sokkal ellenállóbbá válik a nedvességgel, a gombákkal és a rovarokkal szemben. Ezáltal élettartama jelentősen megnő a hagyományos faanyagokhoz képest, ami hosszú távon költséghatékony megoldást jelent.

Nagy keménység és kopásállóság

A muraszta rendkívül kemény és kopásálló, így ideális választás olyan helyekre, ahol nagy a mechanikai igénybevétel, például teraszburkolatokhoz, padlózatokhoz és lépcsőkhöz.

Jobb méretstabilitás

A hőkezelés csökkenti a faanyag nedvességfelvételét és -leadását, ami javítja a méretstabilitását. Ennek köszönhetően a muraszta kevésbé hajlamos a vetemedésre, a repedezésre és a zsugorodásra.

Esztétikus megjelenés

A hőkezelés a faanyag színét mélyebbé és gazdagabbá teszi, kiemelve annak természetes szépségét. A muraszta általában egyenletesebb textúrájú és elegáns megjelenésű.

Környezetbarát megoldás

A muraszta előállítása során nem használnak káros vegyi anyagokat, csupán hőt és gőzt. Emellett a hosszú élettartamának köszönhetően ritkábban kell cserélni, ami csökkenti a hulladék mennyiségét.

Könnyű megmunkálhatóság

Annak ellenére, hogy a muraszta keményebb, mint a hagyományos faanyagok, jól megmunkálható a szokásos faipari szerszámokkal.

Muraszta vásárlása: Mire érdemes odafigyelni?

Ha muraszta vásárlását tervezi, érdemes néhány fontos szempontot figyelembe vennie a megfelelő minőség és a legjobb ár-érték arány elérése érdekében.

A faanyag minősége és a hőkezelés

Győződjön meg arról, hogy a kínált muraszta valóban minőségi keményfából készült, és a hőkezelési eljárást megfelelően hajtották végre. Kérjen tájékoztatást a felhasznált fafajtáról és a hőkezelés paramétereiről.

A méretek és a kiszerelés

Gondolja át, milyen méretű és mennyiségű muraszta termékre van szüksége a projektjéhez. Ellenőrizze a kínált méreteket és a kiszerelési egységeket.

Az ár és a szállítási feltételek

Hasonlítsa össze a különböző forgalmazók árait és szállítási feltételeit. Ne feledje, hogy a legolcsóbb ajánlat nem mindig a legjobb választás, ha a minőség rovására megy. Érdemes tájékozódni a szállítási költségekről és a szállítási időről is.

A forgalmazó megbízhatósága és referenciái

Válasszon megbízható forgalmazót, aki rendelkezik referenciákkal és pozitív vásárlói visszajelzésekkel. Egy jó hírű forgalmazó garanciát jelent a minőségre és a megbízható szállításra.

A felületkezelés

Néhány muraszta termék már felületkezelt állapotban kerül forgalomba (például olajozva vagy viaszolva). Ha ez fontos Önnek, érdeklődjön a kínált felületkezelési lehetőségekről.

A tanácsadás és a szakmai segítség

Egy jó forgalmazó szívesen nyújt szakmai tanácsot a muraszta kiválasztásával és felhasználásával kapcsolatban. Ha bizonytalan a döntésében, kérjen segítséget.

Miért válasszon minket, ha muraszta terméket szeretne vásárolni?

Mi büszkék vagyunk arra, hogy kiváló minőségű muraszta termékeket kínálunk közvetlenül a termelőtől, kedvező áron és széles választékban.

Közvetlenül a termelőtől

Nálunk közvetlenül a termelőtől vásárolhatja meg a muraszta termékeket, így elkerülheti a felesleges közvetítői költségeket és garantáltan a legjobb árat kapja.

Kiváló minőségű faanyagok

Csak a legjobb minőségű keményfa alapanyagokat használjuk fel a muraszta gyártásához, és a hőkezelési eljárást a legszigorúbb szabványoknak megfelelően végezzük.

Széles választék

Kínálatunkban megtal

Uncategorized

Feher Szonyeg Tisztitasa Hazilag

Fehér szőnyeg tisztítása házilag – Vissza a ragyogó fehérség

A fehér szőnyeg otthonunk elegáns és stílusos kiegészítője lehet, azonban köztudottan hajlamosabb a szennyeződésekre és a foltokra, mint sötétebb társai. A mindennapi használat során könnyen előfordulhat, hogy rákerül valamilyen nem kívánt anyag, ami rontja a szőnyeg esztétikai megjelenését. Szerencsére nem feltétlenül szükséges azonnal szakemberhez fordulnunk, hiszen számos hatékony módszer létezik a fehér szőnyeg házilag történő tisztítására. Ebben a részletes útmutatóban bemutatjuk a legfontosabb tudnivalókat, praktikákat és bevált módszereket, amelyek segítségével fehér szőnyegünk újra régi fényében tündökölhet.

Miért olyan nehéz a fehér szőnyeg tisztítása?

A fehér szín önmagában is kihívást jelent a tisztítás terén, hiszen minden apró szennyeződés azonnal láthatóvá válik rajta. A szőnyeg szálai közé bekerült por, morzsák, kiömlött folyadékok vagy éppen a háziállatok által okozott szennyeződések különösen feltűnőek egy fehér szőnyegen. Emellett a különböző anyagokból készült szőnyegek eltérő tisztítási módszereket igényelhetnek, ami tovább bonyolíthatja a helyzetet. A nem megfelelő tisztítószerek vagy technikák alkalmazása pedig akár maradandó károsodást is okozhat a szőnyegben, ezért rendkívül fontos a körültekintő és szakszerű eljárás.

A leggyakoribb folttípusok a fehér szőnyegen

Ahhoz, hogy hatékonyan vehessük fel a harcot a foltokkal szemben, először is érdemes tisztában lennünk a leggyakoribb folttípusokkal, amelyekkel egy fehér szőnyeg tulajdonosának szembe kell néznie:

Kávé- és teafoltok: Az egyik leggyakoribb baleset, különösen reggel vagy vendégvárás közben. A kávé és a tea erős színezőanyagokat tartalmaz, amelyek mélyen beivódhatnak a szőnyeg szálai közé.
Vörösborfoltok: Makacs és nehezen eltávolítható foltok, amelyek azonnali beavatkozást igényelnek. A vörösbor pigmentjei erősen kötődnek a szőnyegrostokhoz.
Ételfoltok: Zsíros, olajos vagy éppen színes szószok okozta foltok, amelyek nemcsak esztétikailag zavaróak, hanem kellemetlen szagot is okozhatnak.
Sárfoltok: Különösen gyakoriak kisgyermekes vagy háziállattal rendelkező családokban. A sár mélyen bejuthat a szőnyeg szálai közé és nehezen távolítható el.

Tinta- és filctollfoltok: Ezek a foltok különösen makacsak lehetnek, és gyakran speciális tisztítószereket igényelnek.
Vérfoltok: Bár ritkábban fordulnak elő, eltávolításuk speciális eljárást igényel.
Háziállatok okozta foltok: A vizelet és a hányás nemcsak foltot hagyhat, hanem kellemetlen szagot és baktériumokat is terjeszthet.

Elsősegély a fehér szőnyegen keletkezett foltoknál

A friss foltok eltávolítása mindig könnyebb, mint a beszáradtaké. Ezért rendkívül fontos, hogy amint észrevesszük a szennyeződést a fehér szőnyegünkön, azonnal cselekedjünk. Íme néhány azonnali lépés, amelyek segíthetnek minimalizálni a károkat:

Azonnali felszívás: Ha folyadék ömlött a szőnyegre, a legfontosabb, hogy minél előbb itassuk fel. Használjunk ehhez tiszta, nedvszívó ruhát vagy papírtörlőt. Óvatosan nyomkodjuk a foltot, ne dörzsöljük, mert ezzel csak mélyebbre préseljük a szennyeződést a szálak közé és növeljük a folt kiterjedését.

Szilárd szennyeződések eltávolítása: Ha szilárd anyag (például sár vagy ételmaradék) került a szőnyegre, először óvatosan kanalazzuk vagy kaparjuk le egy tompa eszközzel (például egy kanállal vagy egy spatulával). Ügyeljünk arra, hogy ne sértsük meg a szőnyeg szálait.
Hideg víz alkalmazása: Sok friss foltot el lehet távolítani hideg vízzel. Nedvesítsünk be egy tiszta ruhát hideg vízzel, és óvatosan töröljük át a foltot kívülről befelé haladva. Ne áztassuk el a szőnyeget!

Házi praktikák a fehér szőnyeg tisztításához

Számos olyan házi szer létezik, amely hatékonyan segíthet a fehér szőnyeg tisztításában. Ezek a módszerek gyakran kíméletesebbek a szőnyeghez és a környezethez, mint a vegyi alapú tisztítószerek. Azonban mindig érdemes először egy kevésbé látható helyen tesztelni a kiválasztott módszert, hogy megbizonyosodjunk arról, hogy nem okoz elszíneződést vagy károsodást.

Ecet és szódabikarbóna csodája

Az ecet és a szódabikarbóna igazi jolly joker a háztartásban, és a fehér szőnyeg tisztításában is kiválóan alkalmazhatók. Ez a kombináció különösen hatékony a szagok eltávolításában és a makacs foltok fellazításában.

Száraz tisztítás szódabikarbónával: Szórjunk bőségesen szódabikarbónát a fehér szőnyeg foltos területére. Hagyjuk hatni legalább néhány órát, vagy akár egy éjszakán át. A szódabikarbóna magába szívja a szennyeződéseket és a kellemetlen szagokat. Ezután alaposan porszívózzuk ki a szőnyeget. Ez a módszer különösen jó zsíros foltokra és általános frissítésre.
Ecetes tisztítás: Keverjünk össze egyenlő arányban fehér ecetet és vizet egy szórófejes flakonban. Fújjuk a keveréket a foltra, majd hagyjuk hatni néhány percig. Ezután óvatosan töröljük át a területet egy tiszta, nedves ruhával. Végül egy száraz ruhával itassuk fel a nedvességet. Az ecet savas kémhatása segít feloldani a szennyeződéseket.
Szódabikarbóna és ecet kombinációja: Makacsabb foltok esetén először szórjunk szódabikarbónát a foltra, majd óvatosan öntsünk rá kevés fehér ecetet. A két anyag reakcióba lép, ami segíthet fellazítani a mélyen ülő szennyeződéseket. Hagyjuk hatni a pezsgést, majd töröljük át a területet egy nedves ruhával, és végül szárítsuk meg.

Citromlé a természetes fehérítő

A citromlé természetes fehérítő hatással rendelkezik, ezért kiválóan alkalmas lehet a fehér szőnyegen keletkezett enyhe foltok és elszíneződések kezelésére. Azonban óvatosan kell használni, és mindig érdemes először egy nem feltűnő helyen tesztelni, mivel savas hatása egyes anyagokat károsíthat.

Alkalmazás: Préseljünk ki friss citromlevet, és vigyük fel közvetlenül a foltra. Hagyjuk hatni néhány percig (ne túl sokáig, hogy ne károsítsa a szálakat), majd óvatosan töröljük át a területet egy nedves ruhával. Végül itassuk fel a nedvességet.
Napfény hatása: Ha a citromlével kezelt szőnyeget kitesszük a napfényre (óvatosan, ne túl erősre és ne túl hosszú időre), az tovább fokozhatja a fehérítő hatást. Ügyeljünk arra, hogy a szőnyeg teljesen megszáradjon a napon.

Só a friss foltok ellen

A só egy kiváló nedvszívó anyag, ezért különösen hatékony lehet a frissen keletkezett folyadékfoltok (például vörösbor) kezelésére a fehér szőnyegen.

Alkalmazás: Amint észrevesszük a foltot, azonnal szórjunk rá bőségesen sót. A só magába szívja a folyadékot, megakadályozva, hogy az mélyebbre hatoljon a szőnyeg szálai közé. Hagyjuk hatni a sót legalább néhány órán át, vagy akár egy éjszakán át, majd alaposan porszívózzuk ki a területet.

Borotvahab a makacs szennyeződésekre

Meglepő lehet, de a borotvahab is segíthet a fehér szőnyeg tisztításában, különösen a makacsabb szennyeződések, például a kávé- vagy teafoltok eltávolításában.

Alkalmazás: Vigyünk fel egy réteg borotvahabot a foltra, és hagyjuk hatni körülbelül 20-30 percig. Ezután óvatosan töröljük át a területet egy nedves ruhával, majd egy száraz ruhával itassuk fel a nedvességet.

Professzionális tisztítószerek és módszerek

Ha a házi praktikák nem hoznak eredményt, vagy ha a fehér szőnyegünk nagyon szennyezett, érdemes lehet speciális szőnyegtisztító szereket vagy professzionális tisztítási módszereket alkalmazni.

Szőnyegtisztító szerek

A boltokban számosféle szőnyegtisztító szer kapható, amelyek kifejezetten a szőnyegek tisztítására és a foltok eltávolítására lettek kifejlesztve. Fontos, hogy fehér szőnyeghez válasszunk olyan terméket, amely nem tartalmaz erős színezőanyagokat, és amely alkalmas a szőnyegünk anyagához.

Használati utasítás: Mindig olvassuk el és kövessük a tisztítószer gyártójának utasításait. Sok terméket hígítani kell vízzel, és csak a foltos területre szabad felvinni.

Tesztelés: Mint a házi praktikáknál, itt is érdemes először egy nem feltűnő helyen tesztelni a tisztítószert, hogy megbizonyosodjunk arról, hogy nem okoz elszíneződést.
Alkalmazás: Vigyük fel a tisztítószert a foltra a használati utasításnak megfelelően, hagyjuk hatni a megadott ideig, majd óvatosan töröljük át a területet egy nedves ruhával. Végül alaposan itassuk fel a nedvességet.

Szőnyegtisztító gépek

A szőnyegtisztító gépek hatékonyabb megoldást nyújthatnak a nagyobb felületű szennyeződések vagy a mélyen beivódott foltok eltávolítására a fehér szőnyegből. Ezek a gépek általában vizet és tisztítószert permeteznek a szőnyegre, majd erőteljesen visszaszívják a szennyezett vizet.

Kölcsönzés vagy vásárlás: Szőnyegtisztító gépeket lehet bérelni vagy vásárolni. Ha gyakran van szükségünk a használatukra, akkor érdemes lehet beruházni egy saját gépre.
Megfelelő tisztítószer: A szőnyegtisztító géphez speciális tisztítószereket kell használni, amelyek nem habzanak túlságosan.
Használat: Kövessük a gép használati utasítását. Általában többször át kell menni a tisztítandó felületen, először a tisztítószeres vízzel, majd csak tiszta vízzel az öblítéshez. A tisztítás után hagyjuk a szőnyeget alaposan megszáradni, lehetőség szerint jól szellőző helyen.

Professzionális szőnyegtisztítás

A legmakacsabb foltokkal vagy a nagyon elhasználódott fehér szőnyegekkel kapcsolatban érdemes lehet professzionális szőnyegtisztító céghez fordulni. A szakemberek speciális gépekkel és tisztítószerekkel rendelkeznek, és nagy tapasztalattal tudják a legnehezebb feladatokat is megoldani. Emellett a professzionális tisztítás meghosszabbíthatja a szőnyeg élettartamát és javíthatja a levegő minőségét otthonunkban.

A fehér szőnyeg megelőző védelme

A legjobb védekezés a támadás, tartja a mondás. Ez a fehér szőnyegre is igaz. Megfelelő megelőző intézkedésekkel jelentősen csökkenthetjük a foltok kialakulásának kockázatát és megőrizhetjük szőnyegünk ragyogó fehérségét.

Lábbelik levétele

Az egyik legegyszerűbb és leghatékonyabb módja a szőnyeg tisztán tartásának, ha a lakásba lépve levesszük a cipőnket. Ezzel megakadályozhatjuk a sár, por és egyéb szennyeződések behordását.

Rendszeres porszívózás

A rendszeres és alapos porszívózás elengedhetetlen a fehér szőnyeg tisztán tartásához. A porszívó eltávolítja a felszíni szennyeződéseket, a port és a morzsákat, mielőtt azok mélyebbre hatolnának a szálak közé. Érdemes hetente legalább kétszer, forgalmasabb helyeken pedig gyakrabban porszívózni.

Azonnali reagálás a kiömlött folyadékokra

Mint már említettük, a friss foltok eltávolítása sokkal könnyebb. Ezért ha valami kiömlik a fe

Uncategorized

Parasztkonyha Berendezese

Miért Válassza a Parasztkonyhát? A Stílus Esszenciája és Előnyei

A parasztkonyha nem csupán egy konyhabútor-stílus, hanem egy életérzés. A vidéki élet nyugalmát, a természet közelségét és a hagyományok tiszteletét testesíti meg. Azok számára, akik vágynak egy olyan konyhára, amely melegséget, otthonosságot és barátságos légkört áraszt, a parasztkonyha ideális választás lehet. Ez a stílus túlmutat a múló divatokon, időtálló eleganciát és funkcionális kényelmet kínálva. A parasztkonyha berendezése során a hangsúly a természetes anyagokon, a kézműves részleteken és a praktikus megoldásokon van, amelyek együttesen egyedi és szerethető teret hoznak létre a mindennapi élethez és a közös étkezésekhez.

A parasztkonyha népszerűségének számos oka van. Először is, a stílus otthonos és hívogató atmoszférát teremt. A fa természetes melegsége, a kerámia és a kő robusztussága, valamint a textíliák lágy esése mind hozzájárulnak egy olyan tér kialakításához, ahol az ember szívesen tölti az idejét. Másodszor, a parasztkonyhák gyakran rendkívül funkcionálisak. A nagyméretű munkafelületek, a bőséges tárolási lehetőségek és a praktikus elrendezés megkönnyítik a főzést és a konyhai munkákat. Harmadszor, a parasztkonyha stílusa sokoldalú, könnyen kombinálható más stílusokkal, így mindenki megtalálhatja a saját ízlésének megfelelő változatot. Végül, de nem utolsósorban, a parasztkonyha egyfajta kapcsolatot teremt a múlttal, a hagyományos értékekkel, ami sokak számára megnyugtató és értékes.

A Parasztkonyha Berendezésének Alapelvei: A Stílus Meghatározó Elemei

A parasztkonyha berendezése nem csupán a bútorok és a kiegészítők kiválasztásáról szól, hanem egy átfogó tervezési folyamat, amely a tér hangulatának és funkcionalitásának megteremtésére irányul. Néhány alapelvet érdemes szem előtt tartani a tökéletes parasztkonyha kialakításához:

Természetes Anyagok Használata: A fa, a kő, a kerámia és a természetes textíliák (pamut, len) dominálnak. Ezek az anyagok nemcsak esztétikusak, hanem tartósak és időtállóak is.
Kézműves Részletek: A kézzel készített vagy antik hatású elemek, mint például a faragott fafrontok, a kovácsoltvas fogantyúk és a kézzel festett kerámiák, egyedi karaktert kölcsönöznek a konyhának.
Funkcionalitás és Praktikusság: A parasztkonyha nemcsak szép, hanem praktikus is. A bőséges tárolási lehetőségek, a nagy munkafelületek és az átgondolt elrendezés elengedhetetlenek.
Meleg és Hívogató Színek: A természetes földszínek, a pasztell árnyalatok és a meleg tónusok dominálnak, amelyek otthonos és barátságos légkört teremtenek.
A Világítás Fontossága: A természetes fény maximalizálása mellett a meleg tónusú mesterséges fényforrások is kulcsszerepet játszanak a hangulat megteremtésében.
Dekoráció és Kiegészítők: A személyes tárgyak, a friss virágok, a fűszernövények és a hagyományos konyhai eszközök mind hozzájárulnak a parasztkonyha egyedi stílusához.

A Konyhabútor Kiválasztása: A Parasztkonyha Szívének Megteremtése

A konyhabútor a parasztkonyha egyik legmeghatározóbb eleme. A megfelelő bútorok kiválasztása nemcsak a konyha megjelenését befolyásolja, hanem a funkcionalitását és a használhatóságát is. Íme néhány szempont, amelyet érdemes figyelembe venni a parasztkonyha bútorainak kiválasztásakor:

Fa Anyagok és Felületek

A fa a parasztkonyha alapanyaga. A tömörfa bútorok nemcsak tartósak és időtállóak, hanem természetes melegséget és eleganciát is sugároznak. Népszerű faanyagok közé tartozik a tölgy, a bükk, a fenyő és a cseresznye. A fa felülete lehet natúr, pácolt, festett vagy antikolt hatású. A natúr fa megőrzi a fa természetes textúráját és színét, míg a pácolt fa mélyebb és gazdagabb árnyalatokat kaphat. A festett fa lehetővé teszi a világosabb, pasztell színek használatát, míg az antikolt hatású felületek a kopottas, régies megjelenést kölcsönöznek a bútoroknak, ami tökéletesen illeszkedik a parasztkonyha stílusához.

A Konyhaszekrények Stílusa és Designja

A konyhaszekrények stílusa nagymértékben meghatározza a parasztkonyha hangulatát. A klasszikus parasztkonyhákra a kazettás ajtók, a profilozott keretek és a díszes fogantyúk jellemzőek. A vitrines szekrények lehetővé teszik a szép edények és dekorációs tárgyak kiállítását, míg a nyitott polcok praktikus tárolási megoldást kínálnak a gyakran használt eszközök számára, és egyben rusztikus megjelenést kölcsönöznek a konyhának. A modern parasztkonyhákban a letisztultabb vonalak és a sima felületek is megjelenhetnek, de a természetes anyagok és a kézműves részletek továbbra is fontos szerepet játszanak.

A Munkalap Kiválasztása

A munkalap nemcsak funkcionális elem, hanem a konyha megjelenésének is fontos része. A parasztkonyhákban gyakran használt munkalapok közé tartozik a tömörfa, a terméskő (gránit, márvány, pala) és a kerámia. A tömörfa munkalap természetes és meleg hatást kelt, de rendszeres karbantartást igényel. A terméskő munkalapok rendkívül tartósak és elegánsak, de általában drágábbak. A kerámia munkalapok könnyen tisztíthatók és sokféle színben és mintában elérhetők, ami lehetővé teszi a stílushoz való illeszkedést.

A Konyhasziget és a Reggelizőpult

Egy konyhasziget vagy egy reggelizőpult nemcsak további munkafelületet és tárolási lehetőséget kínál, hanem a konyha központi elemévé is válhat. A parasztkonyhákban a konyhasziget gyakran masszív fából készül, esetleg kő vagy kerámia munkalappal. A reggelizőpult lehet egy egyszerű fa asztal vagy egy a konyhaszekrényekhez illeszkedő pult, bárszékekkel kiegészítve, ami ideális hely a gyors étkezésekhez és a társasági élethez.

Konyhai Eszközök és Berendezések: A Funkcionalitás és a Stílus Harmóniája

A konyhai eszközök és berendezések kiválasztásakor fontos, hogy a funkcionalitás mellett a stílus is érvényesüljön. A modern készülékek is beilleszthetők a parasztkonyhába, ha a megfelelő designnal rendelkeznek vagy ha ügyesen vannak elrejtve.

Tűzhely és Sütő

A tűzhely a konyha egyik központi eleme. A klasszikus parasztkonyhákban gyakran látni szabadon álló, rusztikus megjelenésű tűzhelyeket, amelyek öntöttvas elemekkel és hagyományos gombokkal rendelkeznek. A modern indukciós vagy kerámialapos tűzhelyek is választhatók, de érdemes olyan modelleket keresni, amelyek designja illeszkedik a paraszti stílushoz, például retro stílusú vagy matt felületű készülékeket. A sütő lehet beépített vagy a tűzhellyel egybeépített, a lényeg, hogy funkcionálisan megfeleljen az igényeknek.

Páraelszívó

A páraelszívó nemcsak a szagok és a pára eltávolításában játszik fontos szerepet, hanem a konyha megjelenését is befolyásolja. A parasztkonyhákba jól illenek a kéményes páraelszívók, amelyek rusztikus hatást keltenek. A beépített páraelszívók kevésbé feltűnőek, de fontos, hogy a burkolatuk a konyha stílusához igazodjon, például fa vagy csempe borítással.

Mosogató és Csaptelep

A mosogató kiválasztásakor a praktikum és az esztétika egyaránt fontos. A kerámia mosogatók, különösen a nagyméretű, egymedencés változatok, tökéletesen illeszkednek a parasztkonyha stílusához. A rozsdamentes acél mosogatók is választhatók, de érdemes matt vagy antikolt felületű modelleket keresni. A csaptelep lehet klasszikus stílusú, bronz vagy réz színű, ami tovább erősíti a rusztikus hatást.

Hűtőszekrény és Fagyasztó

A modern hűtőszekrények és fagyasztók gyakran nem illenek a klasszikus parasztkonyha képébe. Érdemes beépített modelleket választani, amelyeknek az ajtaját a konyhabútor frontjához hasonló panelekkel lehet burkolni, így a készülékek harmonikusan illeszkednek a konyha stílusához. Léteznek retro stílusú, szabadon álló hűtőszekrények is, amelyek egyedi és stílusos kiegészítői lehetnek a parasztkonyhának.

Kisgépek és Konyhai Eszközök

A kisgépek és konyhai eszközök kiválasztásakor érdemes olyan darabokat keresni, amelyek nemcsak funkcionálisak, hanem esztétikusak is. A retro stílusú kenyérpirítók, vízforralók és kávéfőzők jól illenek a parasztkonyha hangulatához. A falra akasztható réz vagy kovácsoltvas edénytartók, a kerámia tárolóedények és a fából készült vágódeszkák mind hozzájárulnak a konyha rusztikus megjelenéséhez.

Színek és Anyagok: A Parasztkonyha Hangulatának Megteremtése

A színek és anyagok kulcsszerepet játszanak a parasztkonyha hangulatának megteremtésében. A természetes és meleg tónusok, valamint a texturált felületek hozzájárulnak az otthonos és barátságos légkör kialakításához.

Földszínek és Pasztell Árnyalatok

A földszínek, mint a bézs, a barna, a szürke és az olívazöld, a parasztkonyha alapját képezik. Ezek a színek nyugalmat és stabilitást sugároznak, és jól harmonizálnak a fa és a kő természetes árnyalataival. A pasztell árnyalatok, mint a halványkék, a rózsaszín és a mentazöld, frissességet és lágyságot visznek a térbe, különösen a kiegészítők és a textíliák terén.

Természetes Anyagok Textúrája

A természetes anyagok textúrája fontos szerepet játszik a parasztkonyha érzékszervi élményében. A fa érdes felülete, a kő hűvössége, a kerámia simasága és a textíliák lágysága mind hozzájárulnak a tér gazdagságához. Érdemes olyan anyagokat választani, amelyek tapintása kellemes és amelyek vizuálisan is érdekesek.

Minták és Motívumok

A minták és motívumok finoman adagolva egyedi karaktert kölcsönözhetnek a parasztkonyhának. A klasszikus paraszti minták közé tartoznak a kockás, a csíkos és a virágos motívumok, amelyek megjelenhetnek a textíliákon, a kerámiákon vagy akár a falburkolaton is. Fontos azonban, hogy a minták ne legyenek túl dominánsak, hanem harmonikusan egészítsék ki a többi elemet.

A Világítás Szerepe a Színek és Anyagok Kiemelésében

A világítás kulcsfontosságú a színek és anyagok szépségének kiemelésében. A természetes fény maximalizálása mellett a meleg tónusú mesterséges fényforrások, mint a függőlámpák, a fali gyertyatartók és az asztali lámpák, otthonos hangulatot teremtenek és kiemelik a konyha textúráit és árnyalatait.

Világítás a Parasztkonyhában: Hangulat és Funkcionalitás Egyensúlya

A világítás a parasztkonyha tervezésének egyik legfontosabb eleme. A megfelelő fényforrások kivá

Építőanyagok

Obi nyitvatartás

Bevezetés az Obi nyitvatartás világába

Az Obi egy vezető barkácsáruház-lánc, amely széles választékot kínál építkezési anyagokból, kertészeti termékekből és lakberendezési kellékekből. Az Obi nyitvatartása kulcsfontosságú információ minden vásárló számára, hiszen a megfelelő időpontokban történő látogatás jelentősen befolyásolhatja a vásárlói élményt. Ebben a cikkben részletesen áttekintjük az Obi nyitvatartását, és hasznos tippeket adunk a vásárlók számára.

Az Obi általános nyitvatartása

Az Obi boltjainak nyitvatartása általában a következőképpen alakul:

Hétfőtől péntekig: 7:00 – 20:00
Szombaton: 7:00 – 18:00
Vasárnap zárva

Ezek az időpontok a legtöbb Obi áruházra érvényesek, de érdemes megjegyezni, hogy egyes helyszínek esetében eltérések lehetnek. Mielőtt útnak indulnánk, javasolt ellenőrizni az adott bolt nyitvatartását online.

Hogyan találjuk meg az Obi legközelebbi boltját?

A legjobb módja annak, hogy megtaláljuk a legközelebbi Obi áruházat, az Obi hivatalos weboldala. Itt a boltkereső funkció segítségével könnyedén beírhatjuk a lakcímünket, és az oldal megmutatja a legközelebbi bolt címét, nyitvatartását, valamint elérhetőségeit.

Különleges nyitvatartási időszakok

Az Obi a különböző ünnepek alatt változó nyitvatartási renddel működik. Például:

Karácsony előtt: a boltok hosszabb nyitvatartással várják a vásárlókat.
Újév: sok áruház zárva tart, így érdemes előre tájékozódni.
Húsvét: szintén különleges nyitvatartással működnek a boltok.

A legfrissebb információkat mindig az Obi hivatalos weboldalán találjuk.

Tippek a vásárláshoz az Obiban

Tervezés: Mielőtt elindulnánk, készítsünk listát a szükséges termékekről. Ez segít elkerülni a felesleges vásárlásokat.
Időzítés: Ha lehetséges, látogassunk el az áruházba hétfőn vagy kedd, mert ilyenkor általában kevesebb a forgalom.
Akciók és kedvezmények: Az Obi gyakran hirdet akciókat, amelyeket érdemes figyelni. Az online hirdetések és hírlevelek hasznos forrást jelenthetnek a legjobb ajánlatokhoz.

Online vásárlás az Obinál

Az Obi nemcsak fizikai boltjaiban, hanem online is lehetőséget kínál vásárlásra. Az online boltban a következő előnyöket élvezhetjük:

Széles választék: Az online boltban sokkal több termék érhető el, mint a fizikai boltban.
Kényelmes vásárlás: A termékeket otthonról rendelhetjük meg, így elkerülhetjük a sorban állást.
Kényelmes házhoz szállítás: A kiválasztott termékeket házhoz is rendelhetjük, ami különösen hasznos nagyobb áruk esetén.

Az Obi ügyfélszolgálata

Az Obi ügyfélszolgálata mindig készen áll, hogy segítsen a vásárlóknak. Legyen szó nyitvatartási időről, akciókról vagy egyéb kérdésekről, az ügyfélszolgálat telefonon és e-mailben is elérhető. Az Obi weboldalán található gyakran ismételt kérdések (GYIK) rész is hasznos információkat nyújt.

Összegzés

Az Obi nyitvatartása fontos szempont minden barkácsolni vágyó vásárló számára. A bolt látogatásának megtervezése előtt érdemes tájékozódni a nyitvatartásról, különösen ünnepi időszakokban. Az online vásárlás lehetősége még kényelmesebbé teszi a vásárlást, és a széles választék révén mindenki megtalálhatja a számára legmegfelelőbb termékeket.

Kivonulhat a Baumax a szomszédból is, az Obi nyelné lé. OBI áruház Kaposvár címe, telefonszáma és szolgáltatásai. A barkácslánc győri áruházának megnyitásával a vállalat mérföldkőhöz érkezett.

Uncategorized

Slovaktual Kosice

A Slovaktual Kassa Világa: Minőségi Ablakok és Ajtók Szakértőktől

Üdvözöljük a Slovaktual Kassa átfogó útmutatójában, ahol a minőségi ablakok és ajtók világa nyílik meg Ön előtt. A Slovaktual név a nyílászárók piacán a megbízhatóságot, az innovációt és a kiváló minőséget képviseli. Kassán és környékén számos otthon és épület büszkélkedhet Slovaktual termékekkel, amelyek nem csupán esztétikusak, hanem hosszú távon is értéket képviselnek.

Miért Válassza a Slovaktual Kassa Termékeit?

A Slovaktual ablakok és ajtók választása számos előnnyel jár. Legyen szó új építésről vagy a meglévő nyílászárók cseréjéről, a Slovaktual termékek a legmagasabb elvárásoknak is megfelelnek. Nézzük meg részletesen, miért érdemes a Slovaktual Kassa kínálatából választani:

Kiváló Minőség és Tartósság

A Slovaktual termékek gyártása során a legkiválóbb alapanyagokat és a legmodernebb technológiákat alkalmazzák. Ez garantálja a termékek hosszú élettartamát és megbízhatóságát. Az ablakok és ajtók ellenállnak az időjárás viszontagságainak, a mechanikai sérüléseknek és a környezeti hatásoknak. A precíz gyártási folyamatnak köszönhetően a Slovaktual nyílászárók évtizedeken át megőrzik eredeti minőségüket.

Innovatív Műszaki Megoldások

A Slovaktual folyamatosan törekszik az innovációra. A kutatás-fejlesztési részleg munkájának köszönhetően a termékek olyan műszaki megoldásokat tartalmaznak, amelyek növelik a komfortot, a biztonságot és az energiahatékonyságot. Ilyen például a többrétegű üvegezés, a speciális profilrendszerek és a biztonsági vasalatok.

Magas Fokú Energiahatékonyság

Napjainkban kiemelten fontos az energiahatékonyság. A Slovaktual Kassa által kínált ablakok és ajtók kiváló hőszigetelő tulajdonságokkal rendelkeznek. Ez jelentősen csökkentheti az otthona fűtési és hűtési költségeit, hozzájárulva ezzel a környezetvédelemhez is. A passzívház szabványoknak megfelelő termékek különösen energiatakarékos megoldást jelentenek.

Esztétikus Megjelenés és Széles Választék

A funkcionalitás mellett a Slovaktual nagy hangsúlyt fektet a termékek esztétikai megjelenésére is. A széles választéknak köszönhetően mindenki megtalálhatja az otthona stílusához leginkább illő ablakokat és ajtókat. A különböző színű és formájú profilok, valamint az egyedi üvegezési lehetőségek lehetővé teszik a személyre szabott megoldások kialakítását.

Biztonság és Védelem

Az otthon biztonsága kiemelten fontos. A Slovaktual ablakok és ajtók magas szintű védelmet nyújtanak a betörések ellen. A speciális biztonsági vasalatok, az erősített profilok és a betörésbiztos üvegezés mind hozzájárulnak ahhoz, hogy otthona biztonságban legyen.

Környezetbarát Gyártás

A Slovaktual elkötelezett a fenntartható fejlődés mellett. A gyártási folyamatok során kiemelt figyelmet fordítanak a környezetvédelmi szempontokra, a hulladék minimalizálására és az erőforrások hatékony felhasználására.

A Slovaktual Kassa Termékkínálata Részletesen

A Slovaktual Kassa széles termékkínálattal várja Önt. Legyen szó ablakokról, bejárati ajtókról, tolóajtókról vagy speciális nyílászárókról, nálunk biztosan megtalálja a megfelelő megoldást.

Műanyag Ablakok

A Slovaktual műanyag ablakai a modern technológia és a kiváló minőség tökéletes ötvözetét képviselik. A többlégkamrás profilrendszerek, a hőszigetelő üvegezés és a precíz tömítések garantálják a magas fokú energiahatékonyságot és a kiváló hangszigetelést. A műanyag ablakok emellett könnyen karbantarthatók és hosszú élettartamúak.

Slovaktual Perfect

A Slovaktual Perfect ablakcsalád a kiváló ár-érték arányt képviseli. A stabil profilrendszer, a kétrétegű hőszigetelő üvegezés és a megbízható vasalatok biztosítják a komfortos lakókörnyezetet.

Slovaktual Komfort

A Slovaktual Komfort ablakok magasabb szintű hőszigetelést és hangszigetelést kínálnak. A háromrétegű üvegezés és a továbbfejlesztett profilrendszer még energiatakarékosabbá teszi otthonát.

Slovaktual Premium

A Slovaktual Premium ablakok a legmagasabb igényeket is kielégítik. A kiváló minőségű alapanyagok, a modern design és a csúcstechnológiás műszaki megoldások garantálják a maximális komfortot és a hosszú élettartamot. A passzívház szabványoknak megfelelő változatok is elérhetők.

Fa Ablakok

A fa ablakok természetes szépséget és eleganciát kölcsönöznek otthonának. A Slovaktual fa ablakai kiváló minőségű fából készülnek, felületkezelésük pedig biztosítja a hosszú távú védelmet az időjárás viszontagságai ellen. A modern hőszigetelő üvegezéssel kombinálva a fa ablakok is kiváló energiahatékonyságot biztosítanak.

Slovaktual Classic

A Slovaktual Classic fa ablakok a hagyományos stílust képviselik modern műszaki megoldásokkal ötvözve. A természetes faanyag meleg és otthonos hangulatot teremt.

Slovaktual Modern

A Slovaktual Modern fa ablakok letisztult vonalvezetésükkel és modern designjukkal illeszkednek a kortárs építészeti stílusokhoz.

Slovaktual Exklusiv

A Slovaktual Exklusiv fa ablakok a luxust és az egyediséget képviselik. A válogatott faanyagok és a részletgazdag kidolgozás garantálják a legmagasabb minőséget.

Alumínium Ablakok

Az alumínium ablakok rendkívül tartósak, stabilak és modern megjelenésűek. A Slovaktual alumínium ablakai kiválóan alkalmasak nagyméretű üvegfelületek kialakítására, emellett pedig magas fokú biztonságot és energiahatékonyságot biztosítanak.

Slovaktual Alu

A Slovaktual Alu ablakcsalád a modern építészet kedvelt eleme. A karcsú profilok és a nagy üvegfelületek világos és tágas tereket teremtenek.

Bejárati Ajtók

A bejárati ajtó nem csupán az otthonunk biztonságát szolgálja, hanem az első benyomást is meghatározza. A Slovaktual Kassa kínálatában megtalálhatók a műanyag, fa és alumínium bejárati ajtók is, melyek mindegyike a legmagasabb minőséget és biztonságot képviseli.

Műanyag Bejárati Ajtók

A Slovaktual műanyag bejárati ajtói tartósak, könnyen karbantarthatók és kiváló hőszigetelő tulajdonságokkal rendelkeznek. A széles választéknak köszönhetően mindenki megtalálhatja az otthonához illő stílust és színt.

Fa Bejárati Ajtók

A fa bejárati ajtók természetes szépséget és eleganciát sugároznak. A Slovaktual fa bejárati ajtói masszív szerkezetükkel és precíz kidolgozásukkal garantálják a biztonságot és a hosszú élettartamot.

Alumínium Bejárati Ajtók

Az alumínium bejárati ajtók rendkívül stabilak és ellenállóak. Modern megjelenésükkel és magas biztonsági szintjükkel ideális választást jelentenek a modern otthonok számára.

Tolóajtók

A tolóajtók praktikus és esztétikus megoldást kínálnak a térkihasználásra és a belső terek összekapcsolására. A Slovaktual Kassa kínálatában megtalálhatók a párhuzamosan eltolható, bukó-toló és emelő-toló ajtók is.

Párhuzamosan Eltolható Ajtók

A párhuzamosan eltolható ajtók helytakarékos megoldást nyújtanak, és lehetővé teszik a nagy üvegfelületek kialakítását.

Bukó-toló Ajtók

A bukó-toló ajtók kombinálják a bukó és a toló funkciókat, így egyszerre biztosítják a szellőztetés és a kijárás lehetőségét.

Emelő-toló Ajtók

Az emelő-toló ajtók a legkényelmesebb és legesztétikusabb megoldást jelentik a nagy üvegfelületek kialakítására. Könnyű kezelhetőségük és kiváló hőszigetelésük miatt népszerű választás.

Speciális Nyílászárók

A Slovaktual Kassa kínálatában megtalálhatók speciális nyílászárók is, mint például a télikert rendszerek, a tűzgátló ajtók és ablakok, valamint az egyedi formájú és méretű nyílászárók.

Télikert Rendszerek

A Slovaktual télikert rendszerei lehetővé teszik egy világos és otthonos élettér kialakítását, amely egész évben használható.

Tűzgátló Ajtók és Ablakok

A Slovaktual tűzgátló ajtói és ablakai a legmagasabb biztonsági előírásoknak is megfelelnek, és értékes időt biztosítanak tűz esetén.

Egyedi Nyílászárók

Ha egyedi elképzelései vannak, a Slovaktual Kassa segít megvalósítani azokat. Egyedi formájú, méretű és kialakítású ablakok és ajtók is rendelhetők.

A Slovaktual Kassa Szolgáltatásai

A Slovaktual Kassa nem csupán minőségi termékeket kínál, hanem átfogó szolgáltatásokkal is áll ügyfelei rendelkezésére.

Szakértői Tanácsadás

Szakértőink segítenek Önnek a megfelelő nyílászárók kiválasztásában, figyelembe véve az Ön igényeit és az épület adottságait. Ingyenes tanácsadással állunk rendelkezésére.

Felmérés és Tervezés

A helyszíni felmérés elengedhetetlen a pontos árajánlat elkészítéséhez és a szakszerű beépítéshez. Tapasztalt munkatársaink elvégzik a szükséges méréseket és segítenek a tervezésben.

Szakszerű Beépítés

A Slovaktual nyílászárók beépítését képzett szakemberek végzik, garantálva a precíz és szakszerű munkát. A helyes beépítés elengedhetetlen a termékek hosszú élettartamához és optimális működéséhez.

Garancia és Szerviz

A Slovaktual termékekre garanciát vállalunk. Emellett szakszerű szervizszolgáltatással is állunk rendelkezésére, ha bármilyen probléma merülne fel.

Referenciák a Slovaktual Kassa Területén

Számos elégedett ügyfelünk van Kassán és környékén, akik már megtapasztalták a Slovaktual termékek minőségét és a szolgáltatásaink színvonalát. Referenciáink megtekinthetők bemutatótermünkben és weboldalunkon.

Lakossági Projektek

Számos családi ház és lakás nyílászáróinak cseréjét végeztük el sikeresen a kassai régióban. Ügyfeleink elégedettek a termékek minőségével, az esztétikai megjelenéssel és az energiahatékonysággal.

Kereskedelmi Projektek

Számos kereskedelmi épület, iroda és üzlethelyiség nyílászáróit is a Slovaktual Kassa szállította és építette be. A tartósság, a biztonság és a modern design kiemelten fontos szempont volt ezeknél a projekteknél.

Közületi Projektek

Oktatási intézmények, egészségügyi létesítmények és más közületi épületek nyílászáróinak cseréjében is részt vettünk. A magas minőség és a speciális követelményeknek való megfelelés volt a legfontosabb szempont.

Lépjen Velünk Kapcsolatba!

Ha felkeltettük érdeklődését, vagy kérdése van a Slovaktual Kassa termékeivel és szolgáltatásaival kapcsolatban, ne habozzon felvenni velünk a kapcsolatot. Szívesen állunk rendelkezésére!

Bemutatóterem Kassán

Látogasson el kassai bemutatótermünkbe, ahol személyesen is megtekintheti termékeinket és konzultálhat szakértőinkkel.

Cím: [Bemutatóterem Címe]

Nyitvatartás: [Nyitvatartási Idő]

Elérhetős

Uncategorized

Szavo Peneszolo Belelegzese

Mi az a Szálló Penész és Hogyan Kerül a Levegőbe?

A penész mikroszkopikus gombák gyűjtőneve, amelyek nedves, organikus anyagokon telepszenek meg és szaporodnak. Számtalan fajtája létezik, és mindegyik apró spórákat bocsát ki a levegőbe. Ezek a penész spórák olyan kicsik, hogy szabad szemmel gyakran nem láthatók, mégis bárhol jelen lehetnek a beltéri és kültéri levegőben egyaránt. A penész akkor kezd el intenzíven szaporodni, ha megfelelő nedvesség áll rendelkezésére, legyen szó beázásról, magas páratartalomról vagy rossz szellőzésről.

Amikor a penész kolóniák megszáradnak vagy megzavarják őket, nagyszámú spóra kerül a levegőbe. Ezek a szálló penész spórák aztán könnyedén belélegezhetők, ami különböző egészségügyi problémákhoz vezethet, különösen érzékeny egyének esetében.

A Szálló Penész Belélegzésének Lehetséges Egészségügyi Hatásai

A szálló penész belélegzése sokféleképpen befolyásolhatja az emberi egészséget. A hatások függhetnek az egyén érzékenységétől, az expozíció mértékétől és a penész fajtájától.

Allergiás Reakciók és Légzőszervi Tünetek

A leggyakoribb reakciók közé tartoznak az allergiás tünetek, mint például tüsszögés, orrfolyás, orrdugulás, köhögés, szemviszketés, könnyezés és bőrkiütések. Az asztmában szenvedők különösen veszélyeztetettek, náluk a szálló penész súlyos asztmás rohamokat válthat ki.

Irritációs Tünetek

Még azoknál is, akik nem allergiásak a penészre, a magas koncentrációban jelen lévő szálló penész spórák irritálhatják a szemet, az orrot és a torkot. Ez különösen igaz lehet rosszul szellőző, nedves környezetben.

Súlyosabb Egészségügyi Problémák

Immunhiányos állapotban lévő vagy krónikus légzőszervi betegségekben szenvedőknél a szálló penész belélegzése súlyosabb fertőzésekhez vezethet. Bizonyos penészfajok, mint például az *Aspergillus*, invazív megbetegedéseket okozhatnak, amelyek azonnali orvosi ellátást igényelnek.

A Penésztoxinok és azok Hatásai

Egyes penészfajok mikotoxinokat termelnek, amelyek mérgező vegyületek. Bár a szálló penész belélegzésével a szervezetbe jutó toxinok mennyisége általában alacsony, hosszan tartó expozíció esetén elméletileg hozzájárulhatnak különböző egészségügyi problémákhoz. A kutatások ezen a területen még folyamatban vannak.

A Szálló Penész Kimutatása és Azonosítása

A szálló penész jelenlétének megállapítása nem mindig egyszerű, mivel a spórák láthatatlanok. Azonban vannak jelek, amelyek utalhatnak a problémára:

Dohos, földszag: Ez gyakran a penész növekedésének első jele.
Látható penészfoltok: Bármilyen színű (fekete, zöld, fehér, stb.) folt a falakon, mennyezeten vagy más felületeken penészre utalhat.
Ismétlődő allergiás tünetek: Különösen, ha a tünetek egy bizonyos helyiségben vagy időszakban felerősödnek.
Nedvességproblémák: Korábbi beázások, magas páratartalom vagy kondenzáció mind kedveznek a penész kialakulásának.

A levegőben lévő penész spórák pontos azonosításához és mennyiségének megállapításához speciális levegőmintavételi tesztek léteznek, amelyeket szakemberek végeznek.

Hatékony Módszerek a Szálló Penész Megelőzésére és Eltávolítására

A szálló penész okozta egészségügyi kockázatok minimalizálása érdekében kulcsfontosságú a megelőzés és a már kialakult penész szakszerű eltávolítása.

A Megelőzés Lépései:

A nedvesség kontrollálása: A legfontosabb a magas páratartalom elkerülése. Használjon páramentesítőt, különösen nedves helyiségekben, mint a fürdőszoba és a konyha.
Jó szellőzés biztosítása: Rendszeresen szellőztesse a lakást, különösen fürdés vagy főzés után. Használjon elszívó ventilátort a fürdőszobában és a konyhában.
Azonnali intézkedés beázás esetén: Ha vízszivárgás vagy beázás történik, a lehető leghamarabb szárítsa fel a területet és javítsa ki a problémát.
Megfelelő szigetelés: A jó szigetelés csökkenti a kondenzáció kialakulásának kockázatát a hideg felületeken.
Rendszeres takarítás: Tartsa tisztán otthonát, különös figyelmet fordítva a nedves területekre.

A Penész Eltávolításának Módszerei:

Kisebb felületeken: Nem porózus felületekről (pl. csempéről) a penész eltávolítható szappanos vízzel vagy speciális penészeltávolító szerekkel. Mindig viseljen védőkesztyűt és légzésvédőt a munka során.
Pórusos felületeken: Olyan anyagokból, mint a gipszkarton vagy a fa, a penész nehezen távolítható el teljesen. Súlyosabb esetben a fertőzött anyagok cseréje lehet a legjobb megoldás.
Szakember segítsége: Nagy kiterjedésű penészfertőzés esetén ajánlott szakemberhez fordulni, aki rendelkezik a megfelelő eszközökkel és tudással a biztonságos és hatékony eltávolításhoz.

Összefoglalás: A Tiszta Beltéri Levegő Fontossága

A szálló penész belélegzése jelentős egészségügyi kockázatot jelenthet, ezért kiemelten fontos a megelőzés és a gyors reagálás a penész megjelenésére. A megfelelő nedvességkontroll, a jó szellőzés és a rendszeres karbantartás mind hozzájárulnak egy egészségesebb beltéri környezet megteremtéséhez. Ne feledje, ha penészt észlel otthonában, ne halogassa a probléma kezelését a saját és családja egészsége érdekében.

Uncategorized

Milyen Belteri Ajtot Vegyek

Milyen Beltéri Ajtót Vegyek? Átfogó Útmutató a Tökéletes Választáshoz

A megfelelő beltéri ajtó kiválasztása kulcsfontosságú döntés otthonunk vagy irodánk kialakításakor. Nem csupán a helyiségek közötti átjárást biztosítják, hanem jelentős szerepet játszanak az esztétikában, a funkcionalitásban és a komfortérzetben is. Egy jól megválasztott belső ajtó képes feldobni egy teret, javítani a hangszigetelést, növelni a biztonságot és hosszú éveken át szolgálni minket. Ebben az átfogó útmutatóban részletesen bemutatjuk a beltéri ajtók széles választékát, segítünk eligazodni a különböző típusok, anyagok, stílusok és méretek között, valamint hasznos tanácsokat adunk a beépítéshez és a karbantartáshoz.

A Beltéri Ajtók Típusai: Funkcionalitás és Stílus Találkozása

A beltéri ajtók sokféle típusa létezik, melyek mindegyike más-más előnyökkel és tulajdonságokkal rendelkezik. A választás során figyelembe kell vennünk a rendelkezésre álló helyet, a funkcionális igényeket és a személyes ízlésünket.

Hagyományos Nyíló Ajtók: Az Időtlen Klasszikus

A hagyományos nyíló ajtók a legelterjedtebb és legismertebb beltéri ajtó típusok. Egy vagy két szárnyból állnak, és egy tengely körül forogva nyílnak és záródnak. Egyszerűségük, megbízhatóságuk és sokoldalúságuk miatt rendkívül népszerűek. Számos anyagból, stílusban és méretben elérhetők, így szinte bármilyen enteriőrhöz megtalálható a megfelelő változat.

Egy- vagy Kétszárnyú Ajtó?

Az, hogy egy- vagy kétszárnyú ajtót választunk, elsősorban a rendelkezésre álló nyílás méretétől és a funkcionális igényektől függ. A egyszárnyú ajtók a leggyakoribbak, kisebb és közepes méretű nyílásokhoz ideálisak. A kétszárnyú ajtók nagyobb nyílásokhoz javasoltak, impozáns megjelenést kölcsönöznek, és szélesebb átjárást biztosítanak, ami különösen hasznos lehet bútorok mozgatásakor.

Tok Típusok: Falcos és Falc Nélküli Megoldások

A nyíló ajtókhoz különböző tok típusok léteznek. A falcos tok esetében az ajtószárny egy peremmel (falccal) illeszkedik a tokba, ami jobb hang- és hőszigetelést biztosít, valamint esztétikailag is egységesebb megjelenést eredményez. A falc nélküli tok modernebb, letisztultabb hatást kelt, mivel az ajtószárny síkban záródik a tokkal.

Tolóajtók: Helytakarékos és Stílusos Megoldás

A tolóajtók kiváló alternatívát jelentenek ott, ahol a hagyományos nyíló ajtók helyszűke miatt problémát okoznának. Az ajtószárny a fal előtt vagy a falban futó sínrendszeren mozog, így nem foglal el értékes alapterületet. A tolóajtók nemcsak praktikusak, hanem modern és stílusos megjelenést is kölcsönöznek a térnek.

Fal előtt Futó Tolóajtók: Egyszerű Beépítés

A fal előtt futó tolóajtók beépítése viszonylag egyszerű, mivel nem igényelnek falbontást. Az ajtószárny egy vagy két sínen fut, és a falra rögzített takaróléc eltakarja a szerkezetet. Számos stílusban és anyagból elérhetők, így könnyen illeszkednek a meglévő enteriőrhöz.

Falban Futó Tolóajtók: Diszkrét Elegancia

A falban futó tolóajtók a legesztétikusabb megoldást nyújtják, mivel a nyitott ajtószárny teljesen eltűnik a falban kialakított tokba. Ez a típusú tolóajtó maximális helymegtakarítást eredményez, és rendkívül letisztult hatást kelt. A beépítése azonban bonyolultabb és falbontással jár.

Harmonika Ajtók: Rugalmas Térfelosztás

A harmonika ajtók több összecsukható panelből állnak, amelyek nyitáskor egymásra tolódnak. Különösen alkalmasak nagyobb nyílások ideiglenes vagy részleges lezárására, illetve terek rugalmas felosztására. Bár kevésbé hangszigetelnek, mint a hagyományos ajtók, praktikus megoldást jelenthetnek bizonyos helyzetekben.

Különleges Funkciójú Beltéri Ajtók

A standard beltéri ajtók mellett léteznek speciális funkciókkal rendelkező változatok is, amelyek bizonyos igények kielégítésére lettek kifejlesztve.

Hangszigetelő Ajtók: A Nyugalom Szigete

A hangszigetelő ajtók speciális szerkezetüknek és anyagaiknak köszönhetően hatékonyan csökkentik a helyiségek közötti zajterjedést. Különösen hasznosak hálószobák, dolgozószobák vagy stúdiók esetében, ahol a csend és a nyugalom kiemelten fontos.

Tűzgátló Ajtók: A Biztonság Záloga

A tűzgátló ajtók speciális anyagokból készülnek és úgy vannak kialakítva, hogy meghatározott ideig ellenálljanak a tűznek és a füstnek. Használatuk kötelező lehet bizonyos épületekben vagy helyiségekben, de otthonunkban is növelhetik a biztonságot.

Nedvességálló Ajtók: Tartósság a Párás Környezetben

A nedvességálló ajtók olyan anyagokból készülnek, amelyek ellenállnak a magas páratartalomnak és a víznek. Különösen ajánlottak fürdőszobákba, WC-kbe vagy más nedves helyiségekbe.

A Beltéri Ajtók Anyagai: Minőség és Esztétika Harmóniája

A beltéri ajtók készülhetnek különböző anyagokból, melyek mindegyike más-más tulajdonságokkal, előnyökkel és hátrányokkal rendelkezik. Az anyagválasztás befolyásolja az ajtó megjelenését, tartósságát, hangszigetelő képességét és árát.

Fa Ajtók: A Természetes Elegancia

A fa ajtók időtlen klasszikusok, amelyek természetes szépségükkel és melegségükkel otthonos hangulatot teremtenek. Készülhetnek tömörfából vagy furnérozott kivitelben.

Tömörfa Ajtók: A Tartósság és a Presztízs Szimbóluma

A tömörfa ajtók a legmagasabb minőséget képviselik. Masszívak, tartósak, kiváló hangszigetelő tulajdonságokkal rendelkeznek, és egyedi, természetes textúrájukkal emelik a tér színvonalát. Ugyanakkor a legdrágábbak is, és érzékenyebbek lehetnek a páratartalom változásaira.

Furnérozott Ajtók: A Megfizethető Fa Elegancia

A furnérozott ajtók MDF vagy faforgács alapra vékony fa furnér réteget ragasztanak. Megjelenésük nagyon hasonlít a tömörfa ajtókhoz, de kedvezőbb áron érhetők el. Viszonylag tartósak és kevésbé érzékenyek a páratartalomra.

MDF Ajtók: A Sokoldalú és Megbízható Választás

Az MDF (közepes sűrűségű farostlemez) ajtók rendkívül népszerűek a jó ár-érték arányuknak és sokoldalúságuknak köszönhetően. Sima, egyenletes felületük ideális a festéshez vagy fóliázáshoz, így számos színben és stílusban elérhetők. Jó hangszigetelő tulajdonságokkal rendelkeznek és tartósak.

Laminált és CPL Ajtók: A Kopásálló és Könnyen Kezelhető Megoldás

A laminált ajtók és a CPL (folyamatos nyomás alatt laminált) ajtók felületét egy speciális, kopásálló műanyag fólia borítja. Ezáltal rendkívül strapabírók, könnyen tisztán tarthatók és ellenállnak a nedvességnek és a karcolásoknak. Számos színben és faerezet mintázattal kaphatók.

Üveg Ajtók: A Fény és a Tér Játéka

Az üveg ajtók modern és elegáns megjelenést kölcsönöznek a térnek, emellett beengedik a természetes fényt, ezáltal világosabbá és tágasabbá teszik a helyiségeket. Készülhetnek teljesen üvegből vagy üvegbetétekkel kombinálva más anyagokkal.

Teljes Üveg Ajtók: A Maximális Fényáteresztés

A teljes üveg ajtók edzett vagy ragasztott biztonsági üvegből készülnek, így biztonságosak a használat során. Különböző mintákkal, textúrákkal vagy akár savmart felülettel is rendelhetők, hogy biztosítsák a megfelelő intimitást.

Üvegbetétes Ajtók: A Stílusos Kombináció

Az üvegbetétes ajtók fa vagy MDF kerettel rendelkeznek, melyekbe különböző méretű és formájú üvegfelületek kerülnek beépítésre. Ez a megoldás ötvözi a fa vagy MDF melegségét az üveg fényáteresztő képességével.

Fém Ajtók: Az Ipari Stílus Kedvelőinek

A fém ajtók robusztus megjelenésükkel és tartósságukkal tűnnek ki. Különösen népszerűek az ipari stílusú enteriőrökben, de modern otthonokban is izgalmas kontrasztot teremthetnek. Készülhetnek acélból vagy alumíniumból, és gyakran kombinálják őket üveggel.

A Beltéri Ajtók Stílusa: Az Otthonunk Hangulatának Meghatározója

A beltéri ajtók stílusa jelentősen befolyásolja otthonunk összképét. A megfelelő stílus kiválasztásakor figyelembe kell vennünk a meglévő berendezést, a falak színét és a padlóburkolatot.

Modern Ajtók: A Letisztult Elegancia

A modern ajtók egyszerű vonalvezetésükkel, minimalista designjukkal és gyakran sima, egyszínű felületükkel tűnnek ki. Jellemzőek a falc nélküli tokok és a rejtett pántok, amelyek tovább erősítik a letisztult hatást. Anyaghasználatukban gyakori az MDF, a laminált felület és az üveg kombinációja.

Klasszikus Ajtók: Az Időtlen Szépség

A klasszikus ajtók gazdagabb díszítéssel, profilozott felületekkel és kazettás kialakítással rendelkeznek. Gyakran készülnek fából vagy furnérozott kivitelben, és a falcos tokok a jellemzőek. A meleg, természetes színek és a hagyományos formák dominálnak.

Rusztikus Ajtók: A Természet Közelsége

A rusztikus ajtók a természetes anyagok és a kézműves hatás jegyében születnek. Jellemző rájuk a durvább felületkezelés, a látható faerezet, a csomók és a repedések. Gyakran készülnek tömörfából, és a robusztus vasalatok tovább erősítik a vidéki hangulatot.

Ipari Stílusú Ajtók: A Loft Hangulat

Az ipari stílusú ajtók a nyers anyagok és a funkcionális design jegyeit hordozzák. Gyakoriak a fémkeretek, az üvegbetétek, a látható csavarok és a kopottas hatású felületek. A tolóajtó változatok különösen népszerűek ebben a stílusban.

Skandináv Stílusú Ajtók: A Világos és Funkcionális Megoldás

A skandináv stílusú ajtók a világos színekre, az egyszerű vonalakra és a természetes anyagokra összpontosítanak. Gyakran készülnek fehérre vagy világos szürkére festett MDF-ből vagy furnérozott fából. A letisztult design és a funkcionalitás a legfontosabb jellemzőik.

A Beltéri Ajtók Méretei: A Pontos Illeszkedés Fontossága

A megfelelő beltéri ajtó méretének kiválasztása elengedhetetlen a problémamentes beépítéshez és a kényelmes használathoz. A szabványos méretek mellett egyedi méretű ajtók is rendelhetők.

Szabvány Méretek: Az Elterjedt Opciók

Magyarországon a beltéri ajtók szabványos méretei általában a következők:

Szélesség: 65 cm, 75 cm, 85 cm, 90 cm, 100 cm
Magasság: 210 cm (tokkal együtt)
Vastagság: 38-45 mm (ajtószárny)

Azonban fontos megjegyezni, hogy a tényleges méretek a gyártótól és a típustól függően eltérhetnek. Mindig pontosan mérjük le a rendelkezésre álló nyílást a vásárlás előtt.

Egyedi Méretek: A Testreszabott Megoldás

Ha a szabványos méretek nem felelnek meg az igényeinknek, lehetőség van egyedi méretű beltéri ajtók rendelésére is. Ez különösen hasznos lehet régi épületek felújításakor, ahol a nyílások nem szabványosak. Az egyedi méretű

Uncategorized

Velux Gzl M06

Miért Válassza a VELUX GZL M06 Tetőtéri Ablakot Otthonába?

A VELUX GZL M06 tetőtéri ablak egy olyan prémium minőségű megoldás, amely ötvözi a funkcionalitást, a tartósságot és az esztétikai megjelenést. Ha Ön természetes fényben gazdag, jól szellőző és energiahatékony tetőtéri helyiséget szeretne kialakítani, akkor ez az ablak ideális választás lehet. Ebben a részletes cikkben bemutatjuk a VELUX GZL M06 minden fontos tulajdonságát, előnyét és műszaki specifikációját, hogy segítsünk Önnek a legjobb döntés meghozatalában.

A VELUX Márka Hírneve és Minősége

A VELUX világszerte elismert név a tetőtéri ablakok piacán. Évtizedek óta kínálnak innovatív és magas minőségű termékeket, amelyek megfelelnek a legszigorúbb építészeti és energetikai követelményeknek. A VELUX ablakok tervezésekor a tartósság, a funkcionalitás és a felhasználói kényelem áll a középpontban. A GZL M06 modell is hűen tükrözi ezt a filozófiát, kiváló minőségű anyagokból készül, és hosszú élettartamra tervezik.

A VELUX GZL M06 Főbb Jellemzői és Műszaki Adatai

A VELUX GZL M06 egy billenőműködésű, fa szerkezetű tetőtéri ablak. A billenő funkció lehetővé teszi az ablak kényelmes nyitását és tisztítását a belső térből. A kiváló minőségű fa alapanyag biztosítja az ablak stabilitását és hosszú élettartamát. Nézzük meg részletesebben a modell legfontosabb jellemzőit:

Méret: Az M06 jelölés egy szabványos méretet takar, amelynek pontos méretei megtalálhatók a VELUX hivatalos dokumentációjában. Ez a méret ideális lehet közepes méretű tetőtéri helyiségekhez, mint például hálószobákhoz, dolgozószobákhoz vagy gyerekszobákhoz.
Üvegezés: A GZL M06 modell általában hőszigetelő üvegezéssel kerül forgalomba, amely kiváló energiahatékonyságot biztosít. A kétrétegű üvegezés csökkenti a hőveszteséget télen és a túlzott felmelegedést nyáron, ezáltal hozzájárulva az alacsonyabb fűtési és hűtési költségekhez. Opcióként elérhető lehet háromrétegű üvegezés is a még jobb hőszigetelés érdekében.
Faanyag: Az ablak kerete és szárnya válogatott, rétegragasztott borovi fenyőből készül. Ez a faanyag rendkívül stabil és ellenálló a deformációval szemben. A felületkezelés védelmet nyújt a nedvesség és a kártevők ellen, biztosítva az ablak hosszú távú tartósságát.
Billenő Működés: A felső kilincses billenőműködés lehetővé teszi az ablak 180 fokos elforgatását, ami megkönnyíti a külső üvegfelület tisztítását. A beépített szellőzőnyílás friss levegőt biztosít a helyiségben anélkül, hogy az ablakot teljesen ki kellene nyitni.
Szellőzőnyílás és Szűrő: A GZL M06 beépített szellőzőnyílással rendelkezik, amely még zárt ablak mellett is lehetővé teszi a folyamatos légcserét. A szellőzőnyílásban található szűrő megakadályozza a por és a rovarok bejutását a helyiségbe.
Kompatibilitás Kiegészítőkkel: A VELUX GZL M06 kompatibilis a VELUX árnyékolóinak, rolóinak és redőnyeinek széles választékával. Ezek a kiegészítők lehetővé teszik a fényerő szabályozását, a hővédelemet és a magánszféra biztosítását.
Beépítési Méretek: A pontos beépítési méreteket mindig a VELUX termékdokumentációjában kell ellenőrizni. Az M06 méret általában egy bizonyos tetőszerkezetbe való beépítésre van optimalizálva.

A VELUX GZL M06 Előnyei Részletesen

A VELUX GZL M06 tetőtéri ablak számos előnyt kínál a felhasználók számára. Ezek az előnyök nemcsak a kényelmet és a funkcionalitást növelik, hanem hozzájárulnak az otthon értékének növeléséhez és az energiaköltségek csökkentéséhez is.

Természetes Fény Bősége

A tetőtéri ablakok egyik legnagyobb előnye a bőséges természetes fény, amelyet beengednek a helyiségbe. A VELUX GZL M06 nagyméretű üvegfelülete maximalizálja a beáramló napfényt, ami világosabbá és barátságosabbá teszi a tetőtéri szobákat. A természetes fény javítja a közérzetet, növeli a termelékenységet és csökkenti a mesterséges világítás iránti igényt, ezáltal energiát takarít meg.

Kiváló Szellőzés

A megfelelő szellőzés elengedhetetlen az egészséges lakókörnyezet megteremtéséhez. A VELUX GZL M06 billenőműködése lehetővé teszi a hatékony és gyors szellőztetést. A felső kilincs segítségével az ablak könnyen nyitható különböző szögben, így szabályozható a beáramló levegő mennyisége. A beépített szellőzőnyílás pedig folyamatos, de huzatmentes légcserét biztosít.

Energiahatékonyság és Hőszigetelés

A modern építészeti trendek és az egyre szigorodó energetikai előírások miatt kiemelten fontos az ablakok hőszigetelő képessége. A VELUX GZL M06 hőszigetelő üvegezéssel rendelkezik, amely minimalizálja a hőveszteséget télen és a hőbejutást nyáron. Ezáltal hozzájárul az épület energiahatékonyságához, csökkenti a fűtési és hűtési költségeket, és kellemes belső hőmérsékletet biztosít egész évben.

Tartósság és Hosszú Élettartam

A VELUX termékei híresek a kiváló minőségű anyaghasználatról és a gondos gyártási folyamatról. A GZL M06 modell is tartós anyagokból készül, amelyek ellenállnak az időjárás viszontagságainak és a mindennapi használatnak. A rétegragasztott fa szerkezet stabilitást biztosít, a felületkezelés pedig védelmet nyújt a nedvesség és a kártevők ellen, így az ablak hosszú éveken át megőrzi eredeti állapotát.

Kényelmes Használat és Tisztítás

A VELUX GZL M06 billenőműködése nemcsak a szellőztetést könnyíti meg, hanem az ablak tisztítását is. Az ablak 180 fokos elforgatásával a külső üvegfelület könnyen hozzáférhetővé válik a belső térből, így biztonságosan és kényelmesen tisztítható. A felső kilincs ergonomikus kialakítású, így az ablak nyitása és zárása egyszerű és kényelmes.

Esztétikus Megjelenés

A VELUX GZL M06 letisztult és modern designja harmonikusan illeszkedik a legtöbb tetőtéri enteriőrhöz. A természetes fa megjelenése melegséget és eleganciát kölcsönöz a helyiségnek. Az ablak formatervezése a funkcionalitást és az esztétikát ötvözi, így nemcsak egy praktikus építőelem, hanem a tér dísze is.

Kompatibilitás Árnyékolókkal és Kiegészítőkkel

A VELUX kiegészítők széles választékát kínálja a GZL M06 modellhez. Ezek közé tartoznak a belső árnyékolók (pliszérolo, fényzáró roló, reluxa), a külső hővédő rolók és a rovarhálók. Ezek a kiegészítők lehetővé teszik a fényerő szabályozását, a hővédelemet, a magánszféra biztosítását és a rovarok távoltartását, növelve a tetőtéri helyiség komfortját és funkcionalitását.

Értéknövelés az Otthon Számára

A minőségi tetőtéri ablakok, mint a VELUX GZL M06, hozzájárulnak az otthon értékének növeléséhez. Egy jól megvilágított, szellőző és energiahatékony tetőtéri helyiség vonzóbbá teszi az ingatlant a potenciális vásárlók számára. A VELUX márka hírneve és a termékek minősége garancia a hosszú távú befektetésre.

A VELUX GZL M06 Összehasonlítása Más Tetőtéri Ablakokkal

A tetőtéri ablakok piacán számos különböző modell és gyártó létezik. A VELUX GZL M06 kiemelkedik a versenytársak közül a kiváló minőségű anyaghasználatnak, a kifinomult műszaki megoldásoknak és a széleskörű kiegészítő választéknak köszönhetően. Összehasonlítva más fa szerkezetű, billenőműködésű ablakokkal, a VELUX GZL M06 gyakran jobb hőszigetelési értékekkel, tartósabb felületkezeléssel és kényelmesebb használattal rendelkezik.

Összehasonlítás a Műanyag Ablakokkal

A műanyag tetőtéri ablakok általában alacsonyabb áron érhetők el, mint a fa ablakok. Azonban a fa ablakok, mint a VELUX GZL M06, gyakran jobb esztétikai megjelenést és természetesebb érzetet nyújtanak. A fa emellett jobb páraszabályozó tulajdonságokkal rendelkezik, ami hozzájárulhat a kellemesebb belső klímához. Bár a műanyag ablakok karbantartása egyszerűbb lehet, a minőségi fa ablakok megfelelő felületkezeléssel szintén hosszú élettartamúak lehetnek.

Összehasonlítás a Középpontos és Felső Tengelyű Ablakokkal

A VELUX GZL M06 egy középpontos billenő ablak. Ez a működési mód lehetővé teszi az ablak könnyű tisztítását és a szellőztetést. A felső tengelyű ablakok nagyobb kilátást biztosíthatnak, de a tisztításuk bonyolultabb lehet. A választás az egyéni preferenciáktól és a beépítési körülményektől függ. A GZL M06 sokoldalúsága miatt népszerű választás a legtöbb tetőtéri alkalmazáshoz.

A VELUX GZL M06 Beépítése és Karbantartása

A VELUX GZL M06 tetőtéri ablak szakszerű beépítése elengedhetetlen a hosszú távú és problémamentes használat érdekében. Javasoljuk, hogy a beépítést képzett szakember végezze, aki rendelkezik a szükséges ismeretekkel és tapasztalattal a VELUX termékek telepítéséhez. A helyes beépítés biztosítja az ablak tökéletes illeszkedését, a megfelelő hőszigetelést és a vízzáróságot.

Beépítési Tanácsok

Előkészítés: A beépítés előtt győződjön meg arról, hogy a tetőszerkezet megfelel az ablak méreteinek és súlyának. Ellenőrizze a VELUX beépítési útmutatóját a pontos követelményekért.
Pozicionálás: Gondolja át, hogy az ablak hol fog a legtöbb természetes fényt beengedni, és hol lesz a legoptimálisabb a szellőzés.
Szakszerű Beépítés: Bízza a beépítést szakemberre, aki ismeri a VELUX technológiát és a helyes beépítési eljárásokat.
Szigetelés: A beépítés során kiemelten fontos a megfelelő szigetelés biztosítása az ablak körül, hogy elkerülje a hőhidak kialakulását és a nedvesség bejutását.

Befejezés: A beépítés után gondoskodjon a belső és külső burkolatok szakszerű kialakításáról.

Karbantartási Útmutató

A VELUX GZL M06 tetőtéri ablak minimális karbantartást igényel. A hosszú élettartam érdekében azonban néhány rendszeres teendőt érdemes elvégezni:

Tisztítás: Rendszeresen tisztítsa meg az ablak üvegfelületét és a keretét enyhe tisztítószeres vízzel és egy puha ronggyal.
Kenés: Évente egyszer ellenőrizze és szükség esetén kenje meg a zsanérokat és a zárszerkezetet.
Tömítések Ellenőrzése: Rendszeresen ellenőrizze az ablak tömítéseit, és ha sérülést vagy kopást tapasztal, cserélje ki őket.
Szellőzőnyílás Szűrőjének Tisztítása: A beépített szellőzőnyílás szűrőjét időnként tisztítsa meg a portól és a szennyeződésektől.
Fa Felületkezelés Ellenőrzése: Időnként ellenőrizze a fa keret felületkezelését

Uncategorized

Auchan Villanybojler

A villanybojler napjaink modern háztartásának elengedhetetlen része. Legyen szó egy gyors kézmosásról, egy frissítő zuhanyról vagy a mosogatásról, a melegvíz iránti igényünk folyamatos. Az Auchan széles kínálatában megtalálható villanybojlerek megbízható és hatékony megoldást nyújtanak otthona melegvíz ellátására. Cikkünkben részletesen bemutatjuk az Auchan villanybojler kínálatának előnyeit, a különböző típusokat és segítünk Önnek a legmegfelelőbb készülék kiválasztásában.

Miért válasszon Auchan villanybojlert?

Számos érv szól amellett, hogy az Auchan kínálatából válasszon villanybojlert. Íme néhány a legfontosabbak közül:

Széles választék: Az Auchan polcain a legkülönfélébb méretű és teljesítményű villanybojlerek megtalálhatók, így biztosan megtalálja az Ön és családja igényeinek leginkább megfelelőt. A kis űrtartalmú készülékektől a nagyobb, családi méretű bojlerekig minden megtalálható.
Megbízható minőség: Az Auchan gondosan válogatja össze kínálatát, így biztos lehet benne, hogy a nálunk kapható villanybojlerek tartósak és megbízhatóan működnek. Számos elismert gyártó terméke megtalálható kínálatunkban.
Energiatakarékosság: A modern Auchan villanybojlerek gyakran rendelkeznek energiatakarékos funkciókkal, amelyek segítenek csökkenteni a villanyszámlát és óvni a környezetet. Érdemes figyelni az energiaosztály besorolására a választás során.
Kedvező árak: Az Auchan híres a kedvező árairól, és ez alól a villanybojler kínálat sem kivétel. Nálunk minőségi termékeket találhat megfizethető áron. Ne feledje rendszeresen figyelemmel kísérni akciós ajánlatainkat sem!
Kényelmes vásárlás: Az Auchan áruházak könnyen megközelíthetők, és a szakértő eladók szívesen segítenek Önnek a választásban. Emellett online is kényelmesen megtekintheti és megrendelheti a kiválasztott villanybojlert.

Különböző típusú Auchan villanybojlerek

Az Auchan kínálatában többféle típusú villanybojler érhető el, hogy mindenki megtalálhassa a számára ideális megoldást:

Fali villanybojlerek

A fali villanybojlerek a legelterjedtebb típusok. Könnyen felszerelhetők a falra, és különböző űrtartalmú változatokban kaphatók. Ideálisak kisebb és nagyobb háztartásokba egyaránt.

Álló villanybojlerek

Az álló villanybojlerek általában nagyobb űrtartalommal rendelkeznek, és nagyobb családok vagy olyan helyek számára ideálisak, ahol nagyobb a melegvíz igény. A padlóra helyezhetők.

Kicsi űrtartalmú villanybojlerek

A kis űrtartalmú villanybojlerek (pl. 5-15 literesek) ideálisak kézmosáshoz vagy kisebb vízigényű helyekre, például vendég WC-be vagy műhelybe.

Indirekt fűtésű villanybojlerek

Az indirekt fűtésű villanybojlerek nem csak elektromos árammal, hanem más hőforrással (pl. központi fűtéssel, napkollektorral) is képesek a vizet felmelegíteni, így energiatakarékos megoldást jelenthetnek.

Hogyan válasszon megfelelő villanybojlert az Auchan kínálatából?

A megfelelő villanybojler kiválasztása fontos döntés. Vegye figyelembe az alábbi szempontokat a választás során:

A háztartás melegvíz igénye: Gondolja át, hányan használják a melegvizet és milyen gyakran. Ez segít meghatározni a szükséges űrtartalmat.

A rendelkezésre álló hely: Mérje le a rendelkezésre álló helyet a bojler felszereléséhez, és válasszon ennek megfelelő méretű és típusú készüléket.
Az energiahatékonyság: Figyeljen a bojler energiaosztályára. Az „A” vagy magasabb besorolású készülékek kevesebb energiát fogyasztanak.
A költségvetés: Határozza meg a rendelkezésre álló összeget, és nézze meg az Auchan kínálatában található, árban megfelelő bojlereket. Ne feledje, a hosszútávú megtakarítás érdekében érdemes lehet egy energiatakarékosabb, de esetleg drágább modellt választani.
További funkciók: Egyes villanybojlerek extra funkciókkal rendelkeznek, mint például a hőmérséklet-szabályozás, a fagyvédelem vagy az intelligens vezérlés. Érdemes átgondolni, hogy ezekre a funkciókra szüksége van-e.

Tippek a villanybojler hatékony használatához

A megfelelő villanybojler kiválasztása mellett fontos a hatékony használat is a költségek csökkentése és a készülék élettartamának meghosszabbítása érdekében:

Állítsa be a megfelelő hőmérsékletet: A túl magas hőmérséklet felesleges energiafogyasztáshoz vezethet. Az ideális hőmérséklet általában 50-60 Celsius-fok között van.
Szigetelje a bojler csöveit: A szigeteléssel csökkentheti a hőveszteséget.
Rendszeresen vízkőtelenítse a bojlert: A vízkő lerakódása csökkenti a bojler hatékonyságát és károsíthatja a fűtőszálat. A rendszeres vízkőtelenítés meghosszabbítja a készülék élettartamát.
Használja az időzítő funkciót (ha van): Állítsa be, hogy a bojler csak akkor melegítse a vizet, amikor valóban szüksége van rá.

Látogasson el az Önhöz legközelebb eső Auchan áruházba vagy tekintse meg online kínálatunkat, és fedezze fel a kiváló minőségű és kedvező árú villanybojlerek széles választékát! Szakértő kollégáink készséggel állnak rendelkezésére, hogy segítsenek Önnek a tökéletes villanybojler kiválasztásában.