Logarithm

A Logaritmus: A Hatványozás Fordított Művelete

A logaritmus egy rendkívül fontos matematikai fogalom, amely szorosan kapcsolódik a hatványozáshoz. Valójában a logaritmus a hatványozás fordított műveleteként definiálható. Segítségével meghatározhatjuk, hogy egy adott alapot milyen kitevőre kell emelnünk ahhoz, hogy egy bizonyos értéket kapjunk.

A Logaritmus Definíciója és Alapvető Elemei

Ha $b^y = x$, ahol $b > 0$ és $b \neq 1$, valamint $x > 0$, akkor az $x$ szám $b$ alapú logaritmusát $y$-nak nevezzük, és ezt így jelöljük: $\log_b(x) = y$. Ebben az egyenletben:

• $b$ a logaritmus alapja. Fontos, hogy az alap pozitív legyen és ne legyen egyenlő 1-gyel.
• $x$ a logaritmus argumentuma vagy száma. Ez mindig pozitív kell, hogy legyen.
• $y$ a logaritmus értéke, amely megadja azt a kitevőt, amelyre az alapot emelve az argumentumot kapjuk.

Példák a Logaritmus Definíciójának Megértéséhez

• $\log_{10}(100) = 2$, mert $10^2 = 100$. Itt az alap 10, az argumentum 100, a logaritmus értéke pedig 2.
• $\log_{2}(8) = 3$, mert $2^3 = 8$. Ebben az esetben az alap 2, az argumentum 8, a logaritmus értéke 3.
• $\log_{e}(e^5) = 5$, mert $e^5 = e^5$. Itt az alap az Euler-szám ($e \approx 2.71828$), az argumentum $e^5$, a logaritmus értéke pedig 5.

A Logaritmus Alapvető Tulajdonságai

A logaritmusok számos fontos tulajdonsággal rendelkeznek, amelyek megkönnyítik a velük való műveleteket és az egyenletek megoldását.

A Szorzat Logaritmusa

Két pozitív szám szorzatának logaritmusa egyenlő a számok logaritmusainak összegével azonos alapon: $\log_b(xy) = \log_b(x) + \log_b(y)$.

A Hányados Logaritmusa

Két pozitív szám hányadosának logaritmusa egyenlő a számláló logaritmusának és a nevező logaritmusának különbségével azonos alapon: $\log_b(\frac{x}{y}) = \log_b(x) – \log_b(y)$.

A Hatvány Logaritmusa

Egy pozitív szám hatványának logaritmusa egyenlő a kitevő és a szám logaritmusának szorzatával azonos alapon: $\log_b(x^p) = p \cdot \log_b(x)$.

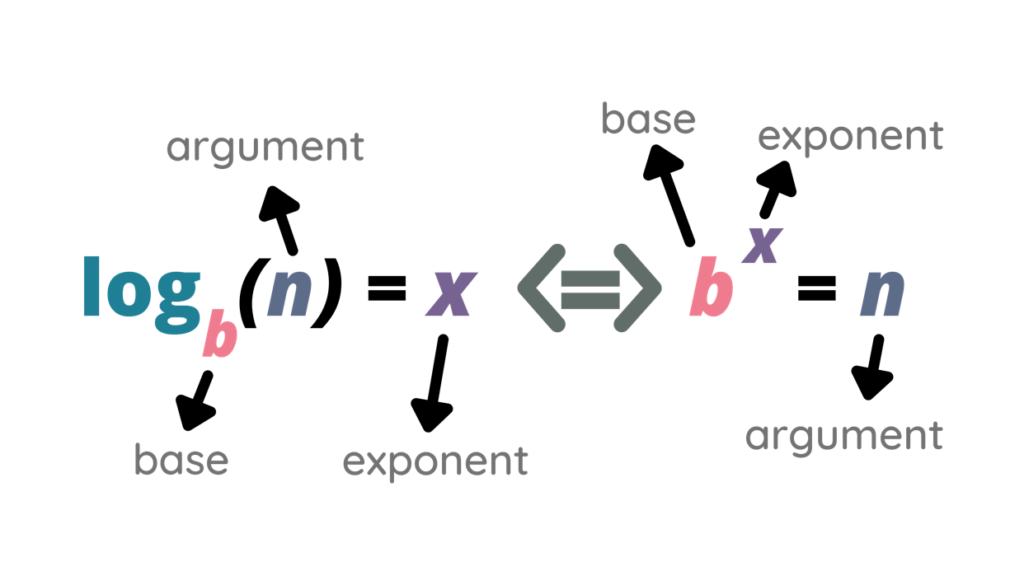
Az Alap Váltása

Gyakran szükség lehet arra, hogy egy logaritmust egy másik alapra váltsunk. Az alapváltás képlete a következő: $\log_a(x) = \frac{\log_b(x)}{\log_b(a)}$, ahol $a, b > 0$ és $a, b \neq 1$. Ezt a képletet gyakran használjuk a számológépekkel történő logaritmusérték-számítás során, mivel a legtöbb számológép csak a 10-es és az $e$ alapú logaritmusokat tudja közvetlenül kiszámítani.

Különleges Logaritmusértékek

• $\log_b(1) = 0$, mert $b^0 = 1$ (minden $b > 0, b \neq 1$ esetén).
• $\log_b(b) = 1$, mert $b^1 = b$ (minden $b > 0, b \neq 1$ esetén).

A Logaritmus Különböző Típusai

A matematikában és a különböző alkalmazásokban gyakran találkozunk speciális alapú logaritmusokkal.

A Természetes Logaritmus

A természetes logaritmus alapja az Euler-szám ($e \approx 2.71828$). Jelölése $\ln(x)$ vagy $\log_e(x)$. A természetes logaritmus rendkívül fontos a matematikában, a fizikában, a mérnöki tudományokban és a közgazdaságtanban, különösen a növekedési és bomlási folyamatok leírásában.

A Tízes Alapú Logaritmus

A tízes alapú logaritmus alapja a 10. Jelölése $\log(x)$ vagy $\log_{10}(x)$. Gyakran használják a tudományos és mérnöki számításokban, különösen a nagyságrendek kifejezésére (például a pH-érték vagy a decibel skála).

A Bináris Logaritmus

A bináris logaritmus alapja a 2. Jelölése $\log_2(x)$ vagy $\text{lb}(x)$. Az informatikában és a számítástechnikában játszik kulcsszerepet, különösen az algoritmusok komplexitásának elemzésében és az információelméletben.

A Logaritmusfüggvény

A logaritmusfüggvény a $f(x) = \log_b(x)$ alakú függvény, ahol $b$ egy rögzített pozitív szám, amely nem egyenlő 1-gyel. A logaritmusfüggvény a exponenciális függvény inverze. Ha $g(x) = b^x$ az exponenciális függvény, akkor $f(x) = \log_b(x)$ a hozzá tartozó logaritmusfüggvény.

A Logaritmusfüggvény Grafikonja és Tulajdonságai

• A logaritmusfüggvény értelmezési tartománya a pozitív valós számok halmaza: $(0, \infty)$.
• Az értékkészlete az összes valós szám halmaza: $(-\infty, \infty)$.
• A függvény áthalad az $(1, 0)$ ponton, mivel $\log_b(1) = 0$.
• Ha $b > 1$, a függvény szigorúan növekvő.
• Ha $0 < b < 1$, a függvény szigorúan csökkenő.

• A logaritmusfüggvénynek függőleges aszimptotája van az $x = 0$ egyenesen.

Logaritmikus Egyenletek és Egyenlőtlenségek

A logaritmikus egyenletek olyan egyenletek, amelyekben a változó a logaritmus argumentumában vagy alapjában szerepel. Ezek megoldása gyakran a logaritmus tulajdonságainak alkalmazását igényli a kifejezések egyszerűsítésére és a változó izolálására.

A logaritmikus egyenlőtlenségek hasonlóak az egyenletekhez, de itt egyenlőség helyett egyenlőtlenségi reláció szerepel. A logaritmikus egyenlőtlenségek megoldásakor figyelembe kell venni a logaritmus alapját, mivel ez befolyásolja az egyenlőtlenség irányát.

A Logaritmus Alkalmazásai a Különböző Területeken

A logaritmus nem csupán egy elméleti matematikai fogalom, hanem számos gyakorlati alkalmazása van a különböző tudományterületeken és a mindennapi életben.

Természettudományok

• Fizika: A hang intenzitásának mérésére használt decibel skála logaritmikus. A csillagok fényességének mérésére használt magnitúdó skála szintén logaritmikus.
• Kémia: A savasság vagy lúgosság mértékét jelző pH-érték egy negatív tízes alapú logaritmus.
• Biológia: A populációdinamikai modellekben gyakran szerepelnek logaritmikus összefüggések a növekedés és a hanyatlás leírására.
• Geológia: A földrengések erősségének mérésére használt Richter-skála logaritmikus.

Mérnöki Tudományok

• Informatika: Az algoritmusok idő- és térbeli komplexitásának elemzésekor gyakran találkozunk logaritmikus függvényekkel (például a bináris keresés komplexitása $O(\log n)$).
• Jelfeldolgozás: A jelek frekvencia-tartományban történő elemzésekor logaritmikus skálákat használnak.
• Vezérléstechnika: A rendszerek stabilitásának elemzésekor Bode-diagramokon logaritmikus skálákat alkalmaznak.

Egyéb Területek

• Közgazdaságtan: A gazdasági növekedés modellezésében és a pénzügyi adatok elemzésében is szerepet játszhat a logaritmus.
• Statisztika: Bizonyos adatok transzformálására használják a logaritmust a normalitás eléréséhez.
• Pszichológia: Az emberi érzékelés bizonyos aspektusai (például a fényerő vagy a hangosság érzékelése) logaritmikus jellegűek (Weber-Fechner törvény).

Összefoglalás

A logaritmus egy alapvető matematikai fogalom, amely a hatványozás inverze. Számos fontos tulajdonsággal rendelkezik, és különböző alapú logaritmusokat különböztetünk meg, mint például a természetes, a tízes alapú és a bináris logaritmust. A logaritmusfüggvény szoros kapcsolatban áll az exponenciális függvénnyel, és számos alkalmazása van a természettudományokban, a mérnöki tudományokban és más területeken. A logaritmikus egyenletek és egyenlőtlenségek megoldása a logaritmus tulajdonságainak alapos ismeretét igényli. A logaritmus megértése elengedhetetlen a matematika és a kapcsolódó tudományterületek mélyebb megértéséhez.