A Fa m3 Számításának Átfogó Útmutatója
A fa m3 számítása kulcsfontosságú mindazok számára, akik a faiparban dolgoznak, tűzifát vásárolnak vagy értékesítenek, esetleg építkezéshez vagy barkácsoláshoz van szükségük faanyagra. A pontos térfogatmeghatározás elengedhetetlen a korrekt árazáshoz, a szállítás tervezéséhez és a különböző faipari folyamatok hatékony végrehajtásához. Ebben a részletes útmutatóban lépésről lépésre bemutatjuk a legfontosabb módszereket és képleteket a fa köbméterének kiszámításához, legyen szó rönkfáról, tűzifáról vagy fűrészáruról.
Miért Fontos a Pontos Fa m3 Számítás?
A pontos fa m3 számítás számos okból kiemelkedő jelentőséggel bír:
- Kereskedelem: A faanyag kereskedelmében a köbméter az egyik legfontosabb mértékegység. A pontos számítás biztosítja a tisztességes árazást mind a vevő, mind az eladó számára.
- Szállítás: A faanyag szállításának tervezésekor elengedhetetlen a pontos térfogat ismerete a megfelelő jármű kiválasztásához és a szállítási költségek kalkulálásához.
- Feldolgozás: A faipari folyamatok során (pl. fűrészelés, gyalulás) a bemenő anyag mennyiségének pontos ismerete elengedhetetlen a hatékony anyagfelhasználáshoz és a termelési tervek elkészítéséhez.
- Tűzifa: A tűzifa vásárlásakor a köbméter segít összehasonlítani a különböző ajánlatokat és biztosítja, hogy a megrendelt mennyiséget kapjuk meg.
- Erdőgazdálkodás: Az erdőgazdálkodásban a kitermelt fa mennyiségének pontos mérése alapvető fontosságú a fenntartható gazdálkodás és a készletgazdálkodás szempontjából.
A Fa m3 Számításának Alapelvei

A fa m3 számítása a faanyag térfogatának meghatározását jelenti köbméterben (m³). A számítás módja függ a faanyag formájától és méretétől. Általánosságban elmondható, hogy a térfogat kiszámításához szükségünk van a faanyag bizonyos méreteire, például a hosszára, átmérőjére vagy kerületére.
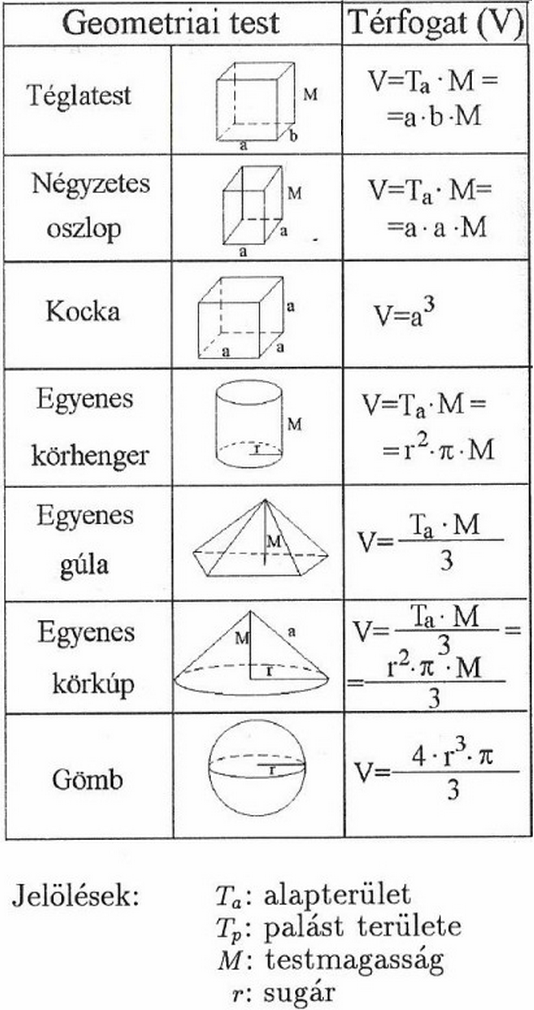
Alapvető Geometriai Képletek a Térfogat Számításához
A fa m3 számításához gyakran használunk alapvető geometriai képleteket:
- Téglatest térfogata: \\text\{Hossz\} \\times \\text\{Szélesség\} \\times \\text\{Magasság\}
- Henger térfogata: \\pi \\times \\text\{Sugár\}^2 \\times \\text\{Magasság\} (ahol a sugár az átmérő fele)
- Kúp térfogata: \\frac\{1\}\{3\} \\times \\pi \\times \\text\{Sugár\}^2 \\times \\text\{Magasság\}
- Gömb térfogata: \\frac\{4\}\{3\} \\times \\pi \\times \\text\{Sugár\}^3
Azonban a faanyagok ritkán rendelkeznek tökéletesen szabályos geometriai formával, ezért speciális módszereket és közelítéseket alkalmazunk a térfogatuk meghatározására.
A Rönkfa m3 Számítása
A rönkfa m3 számítása az egyik leggyakoribb feladat a faiparban és az erdőgazdálkodásban. A rönkök általában hengeres vagy ahhoz közeli formájúak, de gyakran előfordul, hogy a keresztmetszetük nem tökéletesen kör alakú, és a vastagságuk is változhat a hosszuk mentén.
Az Átlagos Keresztmetszet Módszere
Az átlagos keresztmetszet módszere egy gyakran használt eljárás a rönkfa térfogatának becslésére. Ennél a módszernél a rönk két végén és esetleg a közepén megmérik az átmérőt, majd ezekből átlagot számolnak. A térfogatot ezután a következő képlettel számítják ki:

\\text\{Térfogat\} \= \\pi \\times \\left\(\\frac\{d\_1 \+ d\_2 \(\+ d\_3 \+ \.\.\.\)\}\{2 \(vagy több\)\}\\right\)^2 \\times L
ahol d\_1, d\_2, … a mért átmérők, és L a rönk hossza.
Példa az Átlagos Keresztmetszet Módszerére
Tegyük fel, hogy van egy 5 méter hosszú rönkünk. Az egyik végén az átmérő 30 cm (0,3 m), a másik végén pedig 40 cm (0,4 m). Az átlagos átmérő:
\\frac\{0,3 \\text\{ m\} \+ 0,4 \\text\{ m\}\}\{2\} \= 0,35 \\text\{ m\}
A rönk térfogata:
\\text\{Térfogat\} \= \\pi \\times \(0,35 \\text\{ m\}\)^2 \\times 5 \\text\{ m\} \\approx 1,924 \\text\{ m\}^3
Huber-képlet
A Huber-képlet egy másik gyakran használt módszer a rönkfa térfogatának számítására. Ez a képlet a rönk közepén mért átmérőt használja:
\\text\{Térfogat\} \= \\pi \\times \\left\(\\frac\{d\_\{közép\}\}\{2\}\\right\)^2 \\times L \= \\frac\{\\pi \\times d\_\{közép\}^2 \\times L\}\{4\}
ahol d\_\{közép\} a rönk középső átmérője, és L a rönk hossza.
Példa a Huber-képletre
Ha egy 6 méter hosszú rönk középső átmérője 38 cm (0,38 m), akkor a térfogata a Huber-képlet szerint:
\\text\{Térfogat\} \= \\frac\{\\pi \\times \(0,38 \\text\{ m\}\)^2 \\times 6 \\text\{ m\}\}\{4\} \\approx 0,680 \\text\{ m\}^3

Smalian-képlet
A Smalian-képlet pontosabb eredményt adhat, különösen akkor, ha a rönk alakja jelentősen eltér a hengertől. Ez a képlet a rönk két végén mért keresztmetszet területének átlagát veszi figyelembe:

\\text\{Térfogat\} \= \\frac\{A\_1 \+ A\_2\}\{2\} \\times L \= \\frac\{\\pi \\times \(r\_1^2 \+ r\_2^2\)\}\{2\} \\times L \= \\frac\{\\pi \\times \(d\_1^2 \+ d\_2^2\)\}\{8\} \\times L
ahol A\_1 és A\_2 a két vég keresztmetszetének területe, r\_1 és r\_2 a két vég sugara, d\_1 és d\_2 a két vég átmérője, és L a rönk hossza.
Példa a Smalian-képletre
Egy 4 méter hosszú rönk egyik végének átmérője 25 cm (0,25 m), a másik végének átmérője 35 cm (0,35 m). A térfogata a Smalian-képlet szerint:
\\text\{Térfogat\} \= \\frac\{\\pi \\times \(\(0,25 \\text\{ m\}\)^2 \+ \(0,35 \\text\{ m\}\)^2\)\}\{8\} \\times 4 \\text\{ m\} \\approx 0,393 \\text\{ m\}^3
A Hossz Mérése
A rönk hosszának pontos mérése szintén kritikus fontosságú a térfogat helyes meghatározásához. A hosszt általában a rönk két vége között, a tengelyével párhuzamosan mérik. Ügyelni kell arra, hogy a mérőszalag egyenesen fusson, és kövesse a rönk görbületét, ha az jelentős.
Az Átmérő Mérése
Az átmérő mérése a rönk keresztmetszetére merőlegesen történik. Mivel a rönk keresztmetszete gyakran nem tökéletesen kör alakú, ezért legalább két, egymásra merőleges irányban kell megmérni az átmérőt, és ezekből átlagot számítani. A mérést a rönk mindkét végén és szükség esetén a közepén is el kell végezni.
A Tűzifa m3 Számítása
A tűzifa m3 számítása némileg eltér a rönkfa mérésétől, mivel a tűzifa általában különböző méretű és alakú hasábokból áll. A tűzifa mennyiségét gyakran űrméterben (ömlesztett köbméter) vagy kalodában (rakott köbméter) adják meg.
Űrméter (Ömlesztett Köbméter)
Az űrméter vagy ömlesztett köbméter a lazán egymásra dobált tűzifa térfogatát jelenti. Ebben az esetben a faanyag és a közte lévő levegő együttes térfogatát mérjük. Az űrméter nem ad pontos képet a tényleges faanyag mennyiségéről, mivel a hasábok közötti hézagok jelentősek lehetnek.
Kaloda (Rakott Köbméter)
A kaloda vagy rakott köbméter egy meghatározott méretű térfogatot (általában 1 m × 1 m × 1 m) szabályosan egymásra rakott tűzifával tölt meg. A kaloda pontosabb képet ad a faanyag mennyiségéről, mint az űrméter, mivel a hasábok szorosan egymás mellett helyezkednek el, minimalizálva a levegővel töltött teret.
Átváltás Űrméter és Kaloda Között
Az űrméter és a kaloda közötti átváltás nem egzakt, mivel függ a tűzifa hasábok méretétől és alakjától, valamint a rakodás módjától. Általánosságban elmondható, hogy 1 kaloda körülbelül 1,4-1,7 űrméternek felel meg.
A Tűzifa Mennyiségének Becslése
Ha nincs lehetőségünk a tűzifa pontos mérésére (pl. ömlesztve vásároljuk), akkor a tárolási hely méreteiből (hosszúság, szélesség, magasság) becsülhetjük meg a mennyiséget. Fontos azonban figyelembe venni a rakodás sűrűségét és a hasábok közötti hézagokat.
A Fűrészáru m3 Számítása
A fűrészáru m3 számítása viszonylag egyszerű, mivel a fűrészáru (pl. deszkák, gerendák) általában téglatest alakú. A térfogatot a hosszúság, szélesség és vastagság összeszorzásával kapjuk meg.
\\text\{Térfogat\} \= \\text\{Hossz\} \\times \\text\{Szélesség\} \\times \\text\{Vastagság\}
Fontos, hogy a méreteket azonos mértékegységben (pl. méterben) adjuk meg a köbméter eredmény eléréséhez.
Példa a Fűrészáru m3 Számítására
Tegyük fel, hogy van 10 darab deszkánk, amelyek mindegyike 3 méter hosszú, 20 cm (0,2 m) széles és 2,5 cm (0,025 m) vastag. Egy deszka térfogata:
\\text\{Térfogat\}\_\\text\{deszka\} \= 3 \\text\{ m\} \\times 0,2 \\text\{ m\} \\times 0,025 \\text\{ m\} \= 0,015 \\text\{ m\}^3
A 10 deszka együttes térfogata:
\\text\{Térfogat\}\_\\text\{összes\} \= 10 \\times 0,015 \\text\{ m\}^3 \= 0,15 \\text\{ m\}^3
Különleges Fűrészáru Formák
Bizonyos esetekben a fűrészáru nem rendelkezik tökéletes téglatest formával (pl. ék alakú elemek). Ilyenkor a térfogatot a keresztmetszet területének és a hosszúságnak a szorzataként számíthatjuk ki, vagy bonyolultabb geometriai képleteket alkalmazhatunk.
Gyakorlati Tippek a Pontos Fa m3 Számításhoz
A pontos fa m3 számításához néhány gyakorlati tippet érdemes betartani:

- Használjunk pontos mérőeszközöket: A mérőszalag, tolómérő vagy lézeres távolságmérő pontossága befolyásolja a végeredményt.
- Többször mérjünk: Különösen rönkfa esetén, ahol az átmérő változhat, érdemes több helyen megmérni a szükséges méreteket és átlagot számítani.
- Vegye figyelembe a kéreg vastagságát: A rönkfa mérésénél a kéreg is hozzászámítódik a mért átmérőhöz. Ha a tényleges faanyag térfogatára vagyunk kíváncsiak, a kéreg vastagságát le kell vonni.
- Standardizált módszereket alkalmazzunk: A faiparban és az erdőgazdálkodásban gyakran használnak standardizált mérési módszereket és táblázatokat a térfogat meghatározásához. Érdemes ezeket megismerni és alkalmazni.
- Legyünk körültekintőek az űrméter és a kaloda közötti átváltásnál: Mindig tisztázzuk, hogy a tűzifa árajánlat űrméterre vagy kalodára vonatkozik.
Speciális Esetek és Számítási Módszerek
Bizonyos speciális esetekben a fa m3 számítása bonyolultabb lehet, és speciális módszereket igényelhet.